
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 设A(x1,y1),B(x2,y2),则PA、PB的方程分别为x1x+y1y=2,x2x+y2y=2,而PA、PB交于P(x0,y0),由此能求出AB的直线方程,求得M,N的坐标,从而可得三角形的面积,利用基本不等式可求最值.
解答 解:设A(x1,y1),B(x2,y2),
由OA⊥PA,可得切线PA:y-y1=-$\frac{{x}_{1}}{{y}_{1}}$(x-x1),
x12+y12=2,
化简可得x1x+y1y=2,
同理PB的方程x2x+y2y=2,
而PA、PB交于P(x0,y0),
即x1x0+y1y0=2,x2x0+y2y0=2,
可得AB的直线方程为:x0x+y0y=2,
即有M($\frac{2}{{x}_{0}}$,0),N(0,$\frac{2}{{y}_{0}}$),
又S△MON=$\frac{1}{2}$|OM|•|ON|=|$\frac{2}{{x}_{0}{y}_{0}}$|,
又|x0y0|=2|$\frac{{x}_{0}}{2}$•y0|≤$\frac{{{x}_{0}}^{2}}{4}$+y02=1,
则S△MON≥2,
当且仅当|x0|=2|y0|时,△MON的面积的最小值为2.
故选:C.
点评 本题考查直线和圆的位置关系,主要是切线方程的求法,考查三角形的面积的最值,注意运用基本不等式,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
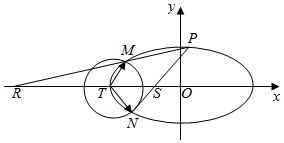 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
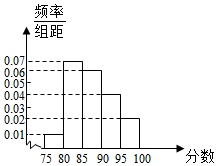 某重点高中拟把学校打造成新兴示范高中,为此制定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),绘制成如图所示的频率分布直方图,已知甲、乙两人同在第3组,丙、丁二人同在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人进行强化培训.
某重点高中拟把学校打造成新兴示范高中,为此制定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),绘制成如图所示的频率分布直方图,已知甲、乙两人同在第3组,丙、丁二人同在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人进行强化培训.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com