
 ij�ص�������ѧУ���������ʾ�����У�Ϊ���ƶ��˺ܶ��µĹ����ƶȣ��¹����ƶ�ʵʩһ��ʱ���ѧУ���¹����ƶ������ȡ100��ѧ�������ʾ����飬���������20�����⣬ÿ������5�֣�����������ɼ��ֳ�5�飻��1��[75��80������2��[80��85������3��[85��90������4��[90��95������5��[95��100�������Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪�ס�������ͬ�ڵ�3�飬����������ͬ�ڵ�4��5�飬�����÷ֲ�����ķ����ڵ�3��4��5�鹲ѡȡ6�˽���ǿ����ѵ��
ij�ص�������ѧУ���������ʾ�����У�Ϊ���ƶ��˺ܶ��µĹ����ƶȣ��¹����ƶ�ʵʩһ��ʱ���ѧУ���¹����ƶ������ȡ100��ѧ�������ʾ����飬���������20�����⣬ÿ������5�֣�����������ɼ��ֳ�5�飻��1��[75��80������2��[80��85������3��[85��90������4��[90��95������5��[95��100�������Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ����֪�ס�������ͬ�ڵ�3�飬����������ͬ�ڵ�4��5�飬�����÷ֲ�����ķ����ڵ�3��4��5�鹲ѡȡ6�˽���ǿ����ѵ������ ��1����Ƶ�ʷֲ�ͼ���ȷֱ����3��4��5����������ɴ�������÷ֲ�����ķ����ڵ�3��4��5�鹲ѡȡ6�˽���ǿ����ѵ����3��4��5��ֱ�ѡȡ��������
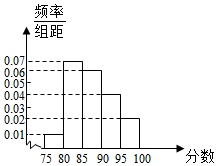
��2������Ƶ�ʷֲ�ֱ��ͼ�������100�˵�ƽ���÷֣�
��3��������X�Ŀ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����Ƶ�ʷֲ�ͼ���ã�
��3������Ϊ��0.06��5��100=30�ˣ�
��4������Ϊ��0.04��5��100=20�ˣ�
��5������Ϊ��0.02��5��100=10�ˣ�
���÷ֲ�����ķ����ڵ�3��4��5�鹲ѡȡ6�˽���ǿ����ѵ��
���3��ѡȡ������Ϊ��30��$\frac{6}{30+20+10}$=3�ˣ�
��4��ѡȡ������Ϊ��20��$\frac{6}{30+20+10}$=2�ˣ�
��5��ѡȡ������Ϊ��10��$\frac{6}{30+20+10}$=1�ˣ�
��2����100�˵�ƽ���÷֣�
$\overline{x}$=0.01��5��77.5+0.07��5��82.5+0.06��5��87.5+0.04��5��92.5+0.02��5��97.5=87.25��
��3���ߵ�3��ѡȡ������Ϊ3�ˣ���4��ѡȡ������Ϊ2�ˣ���5��ѡȡ������Ϊ1�ˣ�
�ס�������ͬ�ڵ�3�飬����������ͬ�ڵ�4��5�飬X��ʾ�ס����������˱�ѡȡ��������
��X�Ŀ���ȡֵΪ0��1��2��3��
P��X=0��=$\frac{{C}_{3}^{0}{C}_{3}^{3}}{{C}_{6}^{3}}$=$\frac{1}{20}$��
P��X=1��=$\frac{{C}_{3}^{1}{C}_{3}^{2}}{{C}_{6}^{3}}$=$\frac{9}{20}$��
P��X=2��=$\frac{{C}_{3}^{2}{C}_{3}^{1}}{{C}_{6}^{3}}$=$\frac{9}{20}$��
P��X=3��=$\frac{{C}_{3}^{3}{C}_{3}^{0}}{{C}_{6}^{3}}$=$\frac{1}{20}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{9}{20}$ | $\frac{9}{20}$ | $\frac{1}{20}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ֲ��м���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24�� | B�� | 60�� | C�� | 48�� | D�� | 36�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
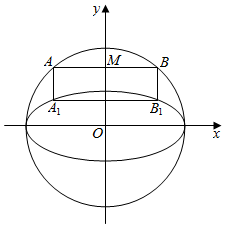 ��ƽ��ֱ������ϵxOy�У���֪ԲO��x2+y2=4����ԲC��$\frac{{x}^{2}}{4}$+y2=1����ֱ��l����M��0��$\frac{3}{2}$������ԲO����A��B���㣬��A��B�ֱ���x��Ĵ��߽���ԲC��A1��B1��A1��A��B1��B����x�����࣮
��ƽ��ֱ������ϵxOy�У���֪ԲO��x2+y2=4����ԲC��$\frac{{x}^{2}}{4}$+y2=1����ֱ��l����M��0��$\frac{3}{2}$������ԲO����A��B���㣬��A��B�ֱ���x��Ĵ��߽���ԲC��A1��B1��A1��A��B1��B����x�����࣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����A��B��C����Բ$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1���������㣬D��OA���е㣬P��Q��ֱ��x=4�ϵ��������㣮
��ͼ����A��B��C����Բ$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1���������㣬D��OA���е㣬P��Q��ֱ��x=4�ϵ��������㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֱ֪��l��y=kx+1����ԲC��$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1��0��b��2����
��ֱ֪��l��y=kx+1����ԲC��$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1��0��b��2�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com