
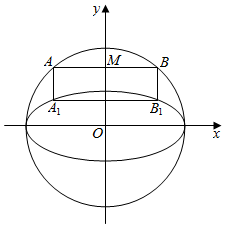
 在平面直角坐标系xOy中,已知圆O:x2+y2=4和椭圆C:$\frac{{x}^{2}}{4}$+y2=1,动直线l过点M(0,$\frac{3}{2}$)且与圆O交于A,B两点,自A,B分别作x轴的垂线交椭圆C于A1,B1,A1与A,B1与B不在x轴的异侧.
在平面直角坐标系xOy中,已知圆O:x2+y2=4和椭圆C:$\frac{{x}^{2}}{4}$+y2=1,动直线l过点M(0,$\frac{3}{2}$)且与圆O交于A,B两点,自A,B分别作x轴的垂线交椭圆C于A1,B1,A1与A,B1与B不在x轴的异侧.分析 (1)考虑直线l的斜率为0,求得交点A,B的坐标,可得直线A1B1经过点(0,$\frac{3}{4}$),猜想直线A1B1过定点(0,$\frac{3}{4}$).设直线l的方程为y=kx+$\frac{3}{2}$,代入圆的方程,可得x的方程;设直线A1B1的方程为y=k'x+$\frac{3}{4}$,代入椭圆x2+4y2=4,可得x的方程,令2k'=k,可得两方程有相同的两根,即可得到定点;
(2)联立两直线方程,求得交点,由2k'=k,即可得到交点在x轴上.
解答 解:(1)当直线l的斜率为0,即l:y=$\frac{3}{2}$,
代入圆O:x2+y2=4,可得交点A(-$\frac{\sqrt{7}}{2}$,$\frac{3}{2}$),B($\frac{\sqrt{7}}{2}$,$\frac{3}{2}$),
令x=±$\frac{\sqrt{7}}{2}$,代入椭圆C:$\frac{{x}^{2}}{4}$+y2=1,可得y=±$\frac{3}{4}$,
由题意可得直线A1B1经过点(0,$\frac{3}{4}$),
猜想直线A1B1过定点(0,$\frac{3}{4}$).
设直线l的方程为y=kx+$\frac{3}{2}$,代入圆x2+y2=4,可得
(1+k2)x2+3kx-$\frac{7}{4}$=0,①
设A(x1,y1),B(x2,y2),
则x1,x2是方程①的两根,
设直线A1B1的方程为y=k'x+$\frac{3}{4}$,
代入椭圆x2+4y2=4,可得(1+4k'2)x2+6k'x-$\frac{7}{4}$=0,②
令2k'=k,则方程①②为同一方程,x1,x2是方程②的两根.
故直线A1B1过定点(0,$\frac{3}{4}$);
(2)证明:由直线y=kx+$\frac{3}{2}$和直线y=k'x+$\frac{3}{4}$,k≠0,
解方程可得x=$\frac{3}{4(k'-k)}$,y=$\frac{3(k-2k')}{4(k-k')}$,
由2k'=k,可得x=-$\frac{3}{2k}$,y=0.
即有直线AB和A1B1相交,交点为(-$\frac{3}{2k}$,0),在x轴上.
点评 本题考查直线和圆、椭圆的位置关系,考查直线恒过定点的求法,注意先运用特殊情况猜想得到定点,考查两直线的交点的特点,考查化简整理的运算能力,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
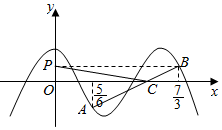 如图,已知函数y=sin($\frac{π}{2}$-πx)的部分图象,点A($\frac{5}{6}$,m),B(${\frac{7}{3}$,n)为函数图象上的点,线段AB与x轴交于点C,及y轴上点P(0,n),则$\overrightarrow{PC}$•$\overrightarrow{AB}$=( )
如图,已知函数y=sin($\frac{π}{2}$-πx)的部分图象,点A($\frac{5}{6}$,m),B(${\frac{7}{3}$,n)为函数图象上的点,线段AB与x轴交于点C,及y轴上点P(0,n),则$\overrightarrow{PC}$•$\overrightarrow{AB}$=( )| A. | $\frac{{25-11\sqrt{3}}}{8}$ | B. | $\frac{{25-9\sqrt{3}}}{8}$ | C. | $\frac{{35-11\sqrt{3}}}{8}$ | D. | $\frac{{35-9\sqrt{3}}}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
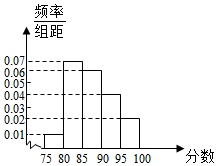 某重点高中拟把学校打造成新兴示范高中,为此制定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),绘制成如图所示的频率分布直方图,已知甲、乙两人同在第3组,丙、丁二人同在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人进行强化培训.
某重点高中拟把学校打造成新兴示范高中,为此制定了很多新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取100名学生进行问卷调查,调查卷共有20个问题,每个问题5分,调查结束后,按成绩分成5组;第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),绘制成如图所示的频率分布直方图,已知甲、乙两人同在第3组,丙、丁二人同在第4,5组,现在用分层抽样的方法在第3,4,5组共选取6人进行强化培训.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}$-y2=1 | B. | x2-$\frac{y^2}{3}$=1 | C. | $\frac{x^2}{6}$-$\frac{y^2}{2}$=1 | D. | $\frac{x^2}{2}$-$\frac{y^2}{6}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15,10,15 | B. | 16,10,14 | C. | 15,11,14 | D. | 16,9,15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2)(3) | B. | (1)(4) | C. | (1)(2)(4) | D. | (1)(3)(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com