
| A. | x=$\frac{5π}{6}$ | B. | x=$\frac{7π}{12}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{6}$ |
分析 利用${∫}_{0}^{\frac{2π}{3}}$f(x)dx=0求出φ值,然后找出使三角函数f(x)取得最值的x即可.
解答 解:函数f(x)=sin(x-φ)且|φ|<$\frac{π}{2}$,
所以${∫}_{0}^{\frac{2π}{3}}$f(x)dx=${∫}_{0}^{\frac{2π}{3}}$sin(x-φ)dx=-cos(x-φ)${|}_{0}^{\frac{2π}{3}}$=-cos($\frac{2π}{3}$-φ)+cosφ=0,
所以tanφ=$\sqrt{3}$,解得φ=$\frac{π}{3}$+kπ,k∈Z;
又|φ|≤$\frac{π}{2}$,∴φ=$\frac{π}{3}$;
所以f(x)=sin(x-$\frac{π}{3}$);
所以函数f(x)的图象的对称轴是x-$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z;
即x=kπ+$\frac{5π}{6}$,k∈Z;
所以f(x)其中一条对称轴为x=$\frac{5π}{6}$.
故选:A.
点评 本题考查了定积分的计算以及三角函数图象对称轴的求法问题,只要使三角函数取得最值的自变量的值,就是三角函数的一条对称轴.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
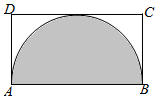 如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )| A. | 1000π | B. | 2000π | C. | 3000π | D. | 400π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos(-α)=-cosα | B. | sin(-α)=-sinα | C. | sin(90°-α)=sinα | D. | cos(90°-α)=cosα |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在等差数列{an}中,若ap+aq=ar+aδ,则p+q=r+δ | |
| B. | 已知数列{an}的前n项和为Sn,若{an}是等比数列,则Sk,S2k-Sk,S3k-S2k也是等比数列 | |
| C. | 在数列{an}中,若ap+aq=2ar,则ap,ar,aq成等差数列 | |
| D. | 在数列{an}中,若ap•aq=a${\;}_{r}^{2}$,则ap,ar,aq成等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=|x| | B. | f(x)=$\frac{1}{x}$ | C. | f(x)=lnx | D. | f(x)=ex |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com