
【题目】已知函数![]()
(1)若对任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)设![]() ,若
,若![]() 没有零点,求实数
没有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)对函数求导得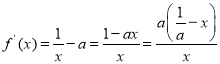 ,通过单调性可知当
,通过单调性可知当![]() 时,函数
时,函数![]() 取得极大值;若对任意
取得极大值;若对任意![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
当且仅当,![]() ,即
,即![]() 恒成立,得
恒成立,得![]() 即
即![]() ,构造函数
,构造函数![]() ,通过单调性求
,通过单调性求![]() 的值.
的值.
(2)![]() ,求导得
,求导得![]()
构造函数![]() ,则
,则![]() 在区间
在区间![]() 内存在唯一零点
内存在唯一零点![]() ,通过单调性求得
,通过单调性求得![]() 的取值范围.
的取值范围.
解:(1)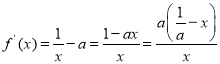 ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() 在
在![]() 上是减函数;
上是减函数;
故当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() .
.
若对任意![]() ,
,![]() 在
在![]() 上恒成立,
上恒成立,
当且仅当,![]() ,即
,即![]() 恒成立,
恒成立,
得![]() 即
即![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 是增函数;
是增函数;
当![]() 时,
时,![]() 是减函数,
是减函数,
所以当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,得
,得![]() .
.
所以![]() ,可得
,可得![]() .
.
(2)![]() ,所以
,所以
![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,
,
所以![]() 在区间
在区间![]() 内存在唯一零点
内存在唯一零点![]() ,
,
即![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上是减函数,
上是减函数,
在![]() 上是增函数,所以
上是增函数,所以![]() .
.
因为![]() 没有零点,所以
没有零点,所以![]() ,
,
即![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一块黄铜板上插着三根宝石针,在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片:每次只能移动一片金片;每次移动的金片必须套在某根针上;大片不能叠在小片上面.设移完n片金片总共需要的次数为an,可推得a1=1,an+1=2an+1.如图是求移动次数在1000次以上的最小片数的程序框图模型,则输出的结果是( )
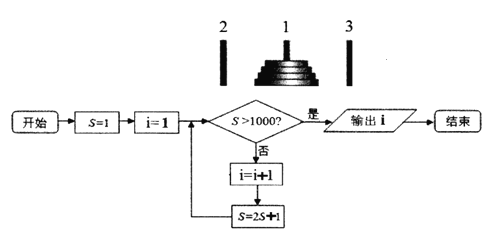
A. 8B. 9C. 10D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
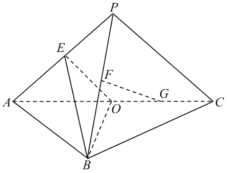
【题目】如图,在三棱锥P—ABC中,平面PAC⊥平面ABC,AB=BC,PA⊥PC.点E,F,O分别为线段PA,PB,AC的中点,点G是线段CO的中点.
(1)求证:FG∥平面EBO;
(2)求证:PA⊥BE.
查看答案和解析>>
科目:高中数学 来源: 题型:
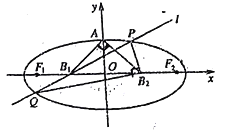
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左右焦点分别为
,左右焦点分别为![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形,过
是面积为4的直角三角形,过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,则直线
,则直线![]() 的斜率为______.
的斜率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,若抛物线
,若抛物线![]() 过点
过点![]() ,且以圆0的切线为准线,
,且以圆0的切线为准线,![]() 为抛物线的焦点,点
为抛物线的焦点,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 与
与![]() 两点,
两点,![]() 关于
关于![]() 轴对称,请问:直线
轴对称,请问:直线![]() 是否过
是否过![]() 轴上的定点,如果不过请说明理由,如果过定点,请求出定点
轴上的定点,如果不过请说明理由,如果过定点,请求出定点![]() 的坐标
的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,边长为a的空间四边形ABCD中,∠BCD=90°,平面ABD⊥平面BCD,则异面直线AD与BC所成角的大小为( )
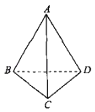
A. 30°B. 45°C. 60°D. 90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名企业为适应发展的需要,计划加大对研发的投入,据了解,该企业原有100名技术人员,年人均投入![]() 万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员
万元,现把原有技术人员分成两部分:技术人员和研发人员,其中技术人员![]() 名(
名(![]() 且
且![]() ),调整后研发人员的年人均投入增加
),调整后研发人员的年人均投入增加![]() %,技术人员的年人均投入调整为
%,技术人员的年人均投入调整为![]() 万元.
万元.
(1)要使这![]() 名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
名研发人员的年总投入恰好与调整前100名技术人员的年总投入相同,求调整后的技术人员的人数;
(2)是否存在这样的实数![]() ,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出
,使得调整后,在技术人员的年人均投入不减少的情况下,研发人员的年总投入始终不低于技术人员的年总投入?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com