
分析 利用正切函数加法定理进行化简,通分合并同类项后,再利用正切加法定理能得到简化的函数式,由正切函数性质能求出最小正周期.
解答 解:f(x)=tan(x+$\frac{π}{4}$)+tan(x-$\frac{π}{4}$)
=$\frac{tanx+tan\frac{π}{4}}{1-tanxtan\frac{π}{4}}$+$\frac{tanx-tan\frac{π}{4}}{1+tanxtan\frac{π}{4}}$
=$\frac{1+tanx}{1-tanx}$+$\frac{tanx-1}{1+tanx}$
=$\frac{ta{n}^{2}x+2tanx+1}{1-ta{n}^{2}x}$-$\frac{ta{n}^{2}x-2tanx+1}{1-ta{n}^{2}x}$
=$\frac{4tanx}{1-ta{n}^{2}x}$
=2tan2x.
∴f(x)=2tan2x,f(x)的最小正周期T=$\frac{π}{2}$.
点评 本题考查三角函数的化简求值,考查三角函数最小正周期的求法,是中档题,解题时要认真审题,注意正切加法定理的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | … | 1 | 2 | 3 | … |
| f(x) | … | 3 | 4 | -1 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
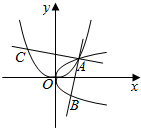 已知抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$.
已知抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com