
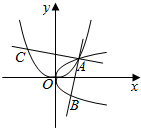
 已知抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$.
已知抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$.分析 (1)由抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$,可得p,进而得到抛物线C2的标准方程;
(2)设出直线AB的方程,联立抛物线C1:y2=$\frac{1}{2}$x,运用韦达定理和弦长公式,求得|AB|,再设直线AC的方程,联立抛物线方程x2=4y,运用韦达定理和弦长公式,可得|AC|,再求m的范围,即可得到.
解答 解:(1)∵抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$,
∴$\sqrt{\frac{1}{64}+\frac{{p}^{2}}{4}}$=$\frac{\sqrt{65}}{8}$,
∴p=2,
∴抛物线C2的标准方程x2=4y;
(2)由C1与C2在第一象限的交点为A,可得A(2,1),
由题意得直线AB的方程为y-1=k(x-2),联立抛物线C1:y2=$\frac{1}{2}$x,消去y,
得k2x2+[2k(1-2k)-$\frac{1}{2}$]x+(1-2k)2=0,
则xAxB=$\frac{(1-2k)^{2}}{{k}^{2}}$,
∵xA=2,∴xB=$\frac{4{k}^{2}-4k+1}{2{k}^{2}}$(k≠$\frac{1}{4}$),
即有|AB|2=(1+k2)|xA-xB|=(1+k2)•|$\frac{4{k}^{2}-4k+1}{2{k}^{2}}$-2|,
直线AC的方程为y-1=-$\frac{1}{k}$(x-2),联立抛物线方程x2=4y,消去y,得kx2+4x-8-4k=0,
∴xAxC=-4-$\frac{8}{k}$,
∵xA=2,∴xC=-2-$\frac{4}{k}$,
即有|AC|2=(1+$\frac{1}{{k}^{2}}$)|xA-xC|=(1+$\frac{1}{{k}^{2}}$)•|-2-$\frac{4}{k}$-2|,
则有m2=($\frac{|\overrightarrow{AB}|}{|\overrightarrow{AC}|}$)2=$\frac{1}{8}$|-4+$\frac{5}{k+1}$|,
∵0<$\frac{5}{k+1}$<5,$\frac{5}{k+1}$≠4,
∴有0<m<$\frac{1}{2}$.
点评 本题考查抛物线的方程和性质,考查直线和抛物线的位置关系,考查韦达定理,以及弦长公式,注意化简整理,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | $\frac{1}{{{{cos}^2}α}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com