
分析 求出f(x)的导数,得f(x)在(a-1,+∞)上是单调减函数.同理,f(x)在(0,a-1)上是单调增函数.求得a≥1,再由g(x)的导数,判断单调性,可得g(x)的最小值,即可得到a的取值范围.
解答 解:函数f(x)=lnx-ax的导数为f′(x)=$\frac{1}{x}$-a,
考虑到f(x)的定义域为(0,+∞),
故a>0,f′(x)<0,解得x>a-1,
即f(x)在(a-1,+∞)上是单调减函数.
同理,f(x)在(0,a-1)上是单调增函数.
由于f(x)在(1,+∞)上是单调减函数,
故(1,+∞)⊆(a-1,+∞),从而a-1≤1,即a≥1.
令g'(x)=ex-a=0,得x=lna.
当x<lna时,g′(x)<0;当x>lna时,g′(x)>0.
又g(x)在(1,+∞)上有最小值,所以lna>1,
即a>e.综上,有a∈(e,+∞).
故答案为:(e,+∞).
点评 本题主要考查了利用函数的导数求出函数的单调性以及函数的极值问题,考查学生分析解决问题的能力,利用导数研究函数的单调性的能力,解题时要认真审题,注意导数性质的合理运用.是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
| x | … | 1 | 2 | 3 | … |
| f(x) | … | 3 | 4 | -1 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
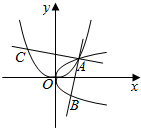 已知抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$.
已知抛物线C1:y2=$\frac{1}{2}$x的焦点与抛物线C2:x2=2px(p>0)的焦点之间的距离为$\frac{\sqrt{65}}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{3}{2}$) | B. | [$\frac{3}{2}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | (-$\frac{3}{2}$,$\frac{3}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com