
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:不详 题型:解答题
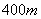 的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?(精确到
的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?(精确到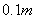 ,取
,取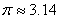 )
)

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用
少热量损耗,管道外表需要覆盖保温层。经测算要覆盖可使用20年的保温层,每厘米厚的保温层材料成本为2万元,小区每年的气量损耗用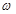 (单位:万元)与保温层厚度
(单位:万元)与保温层厚度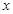 (单位:
(单位: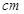 )满足关系:
)满足关系: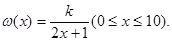 若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为
若不加保温层,每年热量损耗费用为5万元。设保温费用与20年的热量损耗费用之和为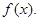
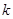 的值及
的值及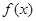 的表达式;
的表达式;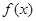 最小,并求最小值。
最小,并求最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
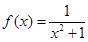 ,令
,令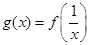 。
。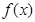 的值域;
的值域;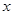 | | | | | | … |
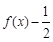 | | | | | | … |
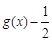 | | | | | | … |
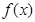 在区间
在区间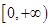 的图像,请据此在该坐标系中补全函数
的图像,请据此在该坐标系中补全函数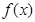 在定义域内的图像,并在同一坐标系中作出函数
在定义域内的图像,并在同一坐标系中作出函数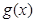 的图像. 请说明你的作图依据.
的图像. 请说明你的作图依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com