
ĄŸÌâÄżĄżŁš1Ł©ÄłĐŁÏÄÁîÓȘÓĐ3ĂûÄĐ͏ѧAĄąBĄąCșÍ3ĂûƟ͏ѧXĄąYĄąZŁŹÆäÄꌶÇéżöÈçϱíŁș
Ò»Äꌶ | ¶țÄꌶ | ÈęÄꌶ | |
ÄĐ͏ѧ | A | B | C |
Ɵ͏ѧ | X | Y | Z |
ÏÖŽÓŐâ6Ăû͏ѧÖĐËæ»úŃĄłö2ÈËČÎŒÓÖȘʶŸșÈü(ĂżÈ˱»ŃĄ”œ”ÄżÉÄÜĐÔÏàÍŹ)Łź
ąÙÓñíÖĐŚÖÄžÁĐŸÙłöËùÓĐżÉÄܔĜáčûŁ»
ąÚÉèMÎȘÊÂŒțĄ°ŃĄłö”Ä2ÈËÀŽŚÔȻ͏ÄꌶÇÒÇĄÓĐ1ĂûÄĐ͏ѧșÍ1ĂûƟ͏ѧĄ±ŁŹÇóÊÂŒțM·ąÉú”ÄžĆÂÊŁź
Łš2Ł©œÚÈŐÇ°ÏŠŁŹĐĄÀîÔÚŒÒĂĆÇ°”ÄÊśÉÏčÒÁËÁœŽźČÊ”ÆŁźŐâÁœŽźČʔƔĔÚÒ»ŽÎÉÁÁÁÏໄ¶ÀÁąŁŹÇÒ¶ŒÔÚÍš”çșó”Ä4ĂëÄÚÈÎһʱżÌ”ÈżÉÄÜ·ąÉúŁŹÈ»șóĂżŽźČÊ”ÆÒÔ4ĂëÎȘŒäžôÉÁÁÁŁźÄÇĂŽŐâÁœŽźČÊ”ÆÍŹÊ±Íš”çșóŁŹËüĂÇ”ÚÒ»ŽÎÉÁÁÁ”ÄʱżÌÏàČîČ»łŹčę2Ăë”ÄžĆÂÊÊǶàÉÙŁż
ĄŸŽđ°žĄżŁš1Ł©ąÙÏêŒûœâÎöąÚ![]() Łš2Ł©
Łš2Ł©![]()
ĄŸœâÎöĄż
Łš1Ł©ąÙÓñíÖĐŚÖÄžÒ»Ò»ÁĐŸÙłöËùÓĐżÉÄܔĜáčûŁŹčČ15žöŁ»
ąÚÓĂÁĐŸÙ·šÇółöÊÂŒț![]() °üșŹ”ÄœáčûÓĐ6žöŁŹ·ûșÏčĆ”äžĆĐÍ”ÄÌŰŐśŁŹÓÉŽËÇó”ĂÊÂŒț
°üșŹ”ÄœáčûÓĐ6žöŁŹ·ûșÏčĆ”äžĆĐÍ”ÄÌŰŐśŁŹÓÉŽËÇó”ĂÊÂŒț![]() ·ąÉú”ÄžĆÂÊŁ»
·ąÉú”ÄžĆÂÊŁ»
Łš2Ł©·ûșÏŒžșΞĆĐÍ”ÄÌŰŐśŁŹÉè”ÚÒ»ŽźČÊ”ÆÁÁ”ÄʱżÌÎȘ![]() ŁŹ”Ú¶țŽźČÊ”ÆÁÁ”ÄʱżÌÎȘ
ŁŹ”Ú¶țŽźČÊ”ÆÁÁ”ÄʱżÌÎȘ![]() ŁŹÓĂČ»”ÈÊœ±íÊŸłöÌőŒțŁŹ»łöÍŒÏóŁŹžùŸĘĂæ»ęÖź±ÈÇółöžĆÂÊŁź
ŁŹÓĂČ»”ÈÊœ±íÊŸłöÌőŒțŁŹ»łöÍŒÏóŁŹžùŸĘĂæ»ęÖź±ÈÇółöžĆÂÊŁź
œâŁșŁš1Ł©ąÙŽÓ6Ăû͏ѧÖĐËæ»úŃĄłö2ÈËČÎŒÓÖȘʶŸșÈü”ÄËùÓĐżÉÄÜœáčûÎȘ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹčČ15ÖÖŁ»
ŁŹčČ15ÖÖŁ»
ąÚŃĄłö”Ä2ÈËÀŽŚÔȻ͏ÄꌶÇÒÇĄÓĐ1ĂûÄĐ͏ѧșÍ1ĂûƟ͏ѧ”ÄËùÓĐżÉÄÜœáčûÎȘ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹčČ6ÖÖŁŹ
ŁŹčČ6ÖÖŁŹ
ÒòŽËŁŹÊÂŒțM·ąÉú”ÄžĆÂÊ![]() Ł»
Ł»
Łš2Ł©Éè”ÚÒ»ŽźČÊ”ÆÁÁ”ÄʱżÌÎȘ![]() ŁŹ”Ú¶țŽźČÊ”ÆÁÁ”ÄʱżÌÎȘ
ŁŹ”Ú¶țŽźČÊ”ÆÁÁ”ÄʱżÌÎȘ![]() ŁŹÔò
ŁŹÔò![]() ŁŹ
ŁŹ
ÒȘÊčÁœŽźČÊ”ÆÁÁ”ÄʱżÌÏàČîČ»łŹčę2Ă룏Ôò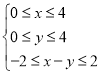 ŁŹ
ŁŹ
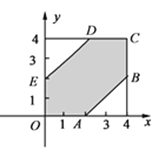
ÈçÍŒŁŹČ»”ÈÊœŚé![]() Ëù±íÊŸ”ÄÍŒĐÎĂæ»ęÎȘ16ŁŹ
Ëù±íÊŸ”ÄÍŒĐÎĂæ»ęÎȘ16ŁŹ
Č»”ÈÊœŚé Ëù±íÊŸ”ÄÁù±ßĐΔÄĂæ»ęÎȘ
Ëù±íÊŸ”ÄÁù±ßĐΔÄĂæ»ęÎȘ![]() ŁŹ
ŁŹ
ÓÉŒžșΞĆĐÍ”Äč«ÊœżÉ”Ă![]() Łź
Łź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżËæŚĆÎÒčúŸŒĂ”Ä·ÉËÙ·ąŐ裏ÈËĂńÉú»îËźÆœ”Ă”œșÜŽóÌážßŁŹÆûł”ÒŃŸœűÈëǧǧÍòÍò”ÄŒÒÍ„.ŽóČż·Ö”Äł”ÖśÔÚčșÂòÆûł”ʱŁŹ»áÔÚœÎł”»òŐß![]() ÖĐŚśłöŃĄÔńŁŹÎȘÁËŃĐŸżÄł”ŰÇűÄÄÖÖł”ĐÍžüÊÜ»¶ÓÒÔŒ°Æûł”Ò»ÄêÄÚ”ÄĐĐÊ»ÀïłÌŁŹÄłÆûł”ÏúÊÛŸÀ팜łöÈçÏÂÍłŒÆŁș
ÖĐŚśłöŃĄÔńŁŹÎȘÁËŃĐŸżÄł”ŰÇűÄÄÖÖł”ĐÍžüÊÜ»¶ÓÒÔŒ°Æûł”Ò»ÄêÄÚ”ÄĐĐÊ»ÀïłÌŁŹÄłÆûł”ÏúÊÛŸÀ팜łöÈçÏÂÍłŒÆŁș
čșÂòÁËœÎł”ŁšÁŸŁ© | čșÂòÁË | |
|
|
|
|
|
|
Łš1Ł©žùŸĘ±íŁŹÊÇ·ńÓĐ![]() ”Ä°ŃÎŐÈÏÎȘÄêÁäÓëčșÂò”ÄÆûł”ł”ĐÍÓĐčŰŁż
”Ä°ŃÎŐÈÏÎȘÄêÁäÓëčșÂò”ÄÆûł”ł”ĐÍÓĐčŰŁż
Łš2Ł©ÍŒžűłö”ÄÊÇ![]() Ăûł”ÖśÉÏÒ»ÄêÆûł””ÄĐĐÊ»ÀïłÌŁŹÇóŐâ
Ăûł”ÖśÉÏÒ»ÄêÆûł””ÄĐĐÊ»ÀïłÌŁŹÇóŐâ![]() Ăûł”ÖśÉÏÒ»ÄêÆûł””ÄÆœŸùĐĐÊ»ÀïłÌŁšÍŹÒ»ŚéÖĐ”ÄÊęŸĘÓÞÌéÇűŒä”ÄÖĐ”ăÖ”ŚśŽú±íŁ©Ł»
Ăûł”ÖśÉÏÒ»ÄêÆûł””ÄÆœŸùĐĐÊ»ÀïłÌŁšÍŹÒ»ŚéÖĐ”ÄÊęŸĘÓÞÌéÇűŒä”ÄÖĐ”ăÖ”ŚśŽú±íŁ©Ł»
Łš3Ł©ÓĂ·ÖČăłéŃù”Ä·œ·šŽÓ![]() ËêÒÔÉÏł”ÖśÖĐłéÈĄ
ËêÒÔÉÏł”ÖśÖĐłéÈĄ![]() ÈËŁŹÔÙŽÓŐâ
ÈËŁŹÔÙŽÓŐâ![]() ÈËÖĐËæ»úłéÈĄ
ÈËÖĐËæ»úłéÈĄ![]() ÈËÔùËÍĂâ·Ń±ŁŃűÈŻŁŹÇóŐâ
ÈËÔùËÍĂâ·Ń±ŁŃűÈŻŁŹÇóŐâ![]() ÈËÖĐÖÁÉÙÓĐ
ÈËÖĐÖÁÉÙÓĐ![]() ÁŸœÎł””ÄžĆÂÊĄŁ
ÁŸœÎł””ÄžĆÂÊĄŁ
žœŁș![]() ŁŹ
ŁŹ![]()
|
|
|
|
|
|
|
|
|
|
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż![]() șșŚÖÌęĐŽŽó»á
șșŚÖÌęĐŽŽó»á![]() Č»¶ÏŽŽÊŐÊÓĐžߣŹÎȘÁ˱ÜĂ⥰ÊéĐŽÎŁ»úĄ±ŁŹșëŃïŽ«ÍłÎÄ»ŻŁŹÄłÊĐŽóÔŒ10ÍòĂûÊĐĂńœűĐĐÁËșșŚÖÌęĐŽČâÊÔ
Č»¶ÏŽŽÊŐÊÓĐžߣŹÎȘÁ˱ÜĂ⥰ÊéĐŽÎŁ»úĄ±ŁŹșëŃïŽ«ÍłÎÄ»ŻŁŹÄłÊĐŽóÔŒ10ÍòĂûÊĐĂńœűĐĐÁËșșŚÖÌęĐŽČâÊÔ![]() ÏÖŽÓÄłÉçÇűŸÓĂńÖĐËæ»úłéÈĄ50ĂûÊĐĂń”ÄÌęĐŽČâÊÔÇéżöŁŹ·ąÏÖ±»ČâÊÔÊĐĂńŐęÈ·ÊéĐŽșșŚÖ”ÄžöÊęÈ«ČżÔÚ160”œ184ÖźŒäŁŹœ«ČâÊÔœáčû°ŽÈçÏ·œÊœ·ÖłÉÁùŚéŁș”Ú1Śé
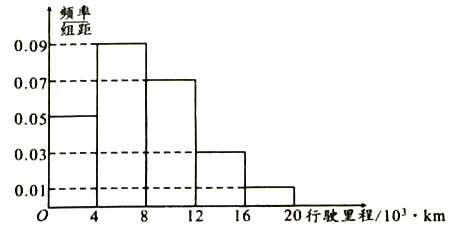
ÏÖŽÓÄłÉçÇűŸÓĂńÖĐËæ»úłéÈĄ50ĂûÊĐĂń”ÄÌęĐŽČâÊÔÇéżöŁŹ·ąÏÖ±»ČâÊÔÊĐĂńŐęÈ·ÊéĐŽșșŚÖ”ÄžöÊęÈ«ČżÔÚ160”œ184ÖźŒäŁŹœ«ČâÊÔœáčû°ŽÈçÏ·œÊœ·ÖłÉÁùŚéŁș”Ú1Śé![]() ŁŹ”Ú2Śé
ŁŹ”Ú2Śé![]() ŁŹ
ŁŹ![]() ŁŹ”Ú6Śé
ŁŹ”Ú6Śé![]() ŁŹÈçÍŒÊÇ°ŽÉÏÊö·ÖŚé·œ·š”Ă”œ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁź
ŁŹÈçÍŒÊÇ°ŽÉÏÊö·ÖŚé·œ·š”Ă”œ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁź

![]() Èô”çÊÓÌšŒÇŐßÒȘŽÓłéÈĄ”ÄÊĐĂńÖĐŃĄ1ÈËœűĐĐČÉ·ĂŁŹÇó±»ČÉ·ĂÈËÇĄșĂÔÚ”Ú2Śé»ò”Ú6Śé”ÄžĆÂÊŁ»
Èô”çÊÓÌšŒÇŐßÒȘŽÓłéÈĄ”ÄÊĐĂńÖĐŃĄ1ÈËœűĐĐČÉ·ĂŁŹÇó±»ČÉ·ĂÈËÇĄșĂÔÚ”Ú2Śé»ò”Ú6Śé”ÄžĆÂÊŁ»
![]() ÊÔčÀŒÆžĂÊĐÊĐĂńŐęÈ·ÊéĐŽșșŚÖ”ÄžöÊę”ÄÆœŸùÊęÓëÖĐλÊꣻ
ÊÔčÀŒÆžĂÊĐÊĐĂńŐęÈ·ÊéĐŽșșŚÖ”ÄžöÊę”ÄÆœŸùÊęÓëÖĐλÊꣻ
![]() ÒŃÖȘ”Ú4ŚéÊĐĂńÖĐÓĐ3ĂûÄĐĐÔŁŹŚéÖŻ·œÒȘŽÓ”Ú4ŚéÖĐËæ»úłéÈĄ2ĂûÊĐĂńŚéłÉșëŃïŽ«ÍłÎÄ»ŻĐûŽ«¶ÓŁŹÇóÖÁÉÙÓĐ1ĂûĆźĐÔÊĐĂń”ÄžĆÂÊŁź
ÒŃÖȘ”Ú4ŚéÊĐĂńÖĐÓĐ3ĂûÄĐĐÔŁŹŚéÖŻ·œÒȘŽÓ”Ú4ŚéÖĐËæ»úłéÈĄ2ĂûÊĐĂńŚéłÉșëŃïŽ«ÍłÎÄ»ŻĐûŽ«¶ÓŁŹÇóÖÁÉÙÓĐ1ĂûĆźĐÔÊĐĂń”ÄžĆÂÊŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚ¶àĂæÌćABD©A1B1C1D1ÖĐËıßĐÎA1B1C1D1ŁŹADD1A1ŁźABB1A1ŸùÎȘŐę·œĐÎŁź”ăMÊÇBD”ÄÖД㣟”ăHÔÚÏ߶ÎC1MÉÏŁŹÇÒA1HÓëÆœĂæABDËùłÉœÇ”ÄŐęÏÒÖ”ÎȘ![]() Łź
Łź
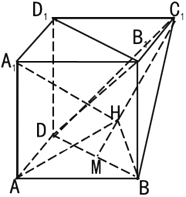
ŁšąńŁ©Ö€ĂśŁșB1D1ĄÎÆœĂæBC1DŁș
ŁšąòŁ©Çó¶țĂæœÇA©A1H©B”Ä”ÄŐęÏÒÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÉèPÊÇÍÖÔČ![]() ÉÏÒ»”㣏MŁŹN·Ö±đÊÇÁœÔČ(xŁ«4)2Ł«y2Łœ1șÍ(xŁ4)2Ł«y2Łœ1ÉÏ”Ä”ăŁŹÔò|PM|Ł«|PN|”ÄŚîĐĄÖ”ĄąŚîŽóÖ”·Ö±đÎȘ Łš Ł©
ÉÏÒ»”㣏MŁŹN·Ö±đÊÇÁœÔČ(xŁ«4)2Ł«y2Łœ1șÍ(xŁ4)2Ł«y2Łœ1ÉÏ”Ä”ăŁŹÔò|PM|Ł«|PN|”ÄŚîĐĄÖ”ĄąŚîŽóÖ”·Ö±đÎȘ Łš Ł©
A. 9,12 B. 8,11 C. 10,12 D. 8,12
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÉèPÊÇÍÖÔČ![]() ÉÏÒ»”㣏MŁŹN·Ö±đÊÇÁœÔČ(xŁ«4)2Ł«y2Łœ1șÍ(xŁ4)2Ł«y2Łœ1ÉÏ”Ä”ăŁŹÔò|PM|Ł«|PN|”ÄŚîĐĄÖ”ĄąŚîŽóÖ”·Ö±đÎȘ Łš Ł©
ÉÏÒ»”㣏MŁŹN·Ö±đÊÇÁœÔČ(xŁ«4)2Ł«y2Łœ1șÍ(xŁ4)2Ł«y2Łœ1ÉÏ”Ä”ăŁŹÔò|PM|Ł«|PN|”ÄŚîĐĄÖ”ĄąŚîŽóÖ”·Ö±đÎȘ Łš Ł©
A. 9,12 B. 8,11 C. 10,12 D. 8,12
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘŐęÈęœÇĐÎ![]() ”ı߳€ÎȘ3ŁŹ
”ı߳€ÎȘ3ŁŹ![]() ·Ö±đÊÇ
·Ö±đÊÇ![]() ±ßÉÏ”Ä”ăŁŹÂúŚă
±ßÉÏ”Ä”ăŁŹÂúŚă![]() (ÈçÍŒ1)Łźœ«
(ÈçÍŒ1)Łźœ«![]() ŐÛÆđ”œ
ŐÛÆđ”œ![]() ”ÄλÖĂŁŹÊčÆœĂæ
”ÄλÖĂŁŹÊčÆœĂæ![]() ÆœĂæ
ÆœĂæ![]() ŁŹÁŹœÓ
ŁŹÁŹœÓ![]() (ÈçÍŒ2)Łź
(ÈçÍŒ2)Łź
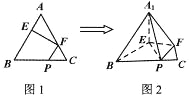
(1)ÇóÖ€Łș![]() ÆœĂæ
ÆœĂæ![]() Ł»
Ł»
(2)Çó¶țĂæœÇ![]() ”ÄÓàÏÒÖ”Łź
”ÄÓàÏÒÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘÊęÁĐ![]() ”ÄÇ°
”ÄÇ°![]() ÏîșÍÎȘ
ÏîșÍÎȘ![]() .ÊęÁĐ
.ÊęÁĐ![]() ÂúŚă
ÂúŚă![]() ŁŹ
ŁŹ![]() .
.
Łš1Ł©Èô![]() ŁŹÇÒ
ŁŹÇÒ![]() ŁŹÇóŐęŐûÊę
ŁŹÇóŐęŐûÊę![]() ”ÄÖ”Ł»
”ÄÖ”Ł»
Łš2Ł©ÈôÊęÁĐ![]() ŁŹ
ŁŹ![]() ŸùÊÇ”ÈČîÊęÁĐŁŹÇó
ŸùÊÇ”ÈČîÊęÁĐŁŹÇó![]() ”ÄÈĄÖ”·¶Î§Ł»
”ÄÈĄÖ”·¶Î§Ł»
Łš3Ł©ÈôÊęÁĐ![]() ÊǔȱÈÊęÁĐŁŹč«±ÈÎȘ
ÊǔȱÈÊęÁĐŁŹč«±ÈÎȘ![]() ŁŹÇÒ
ŁŹÇÒ![]() ŁŹÊÇ·ńŽæÔÚŐęŐûÊę
ŁŹÊÇ·ńŽæÔÚŐęŐûÊę![]() ŁŹÊč
ŁŹÊč![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() łÉ”ÈČîÊęÁĐŁŹÈôŽæÔÚŁŹÇółöÒ»žö
łÉ”ÈČîÊęÁĐŁŹÈôŽæÔÚŁŹÇółöÒ»žö![]() ”ÄÖ”ŁŹÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉ.
”ÄÖ”ŁŹÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉ.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșžßÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłč€ł§¶ÔÒ»ĆúČúÆ·œűĐĐÁËłéŃùŒìČâ.ÓÒÍŒÊÇžùŸĘłéŃùŒìČâșó”ÄČúÆ·Ÿ»ÖŰŁš”„λŁșżËŁ©ÊęŸĘ»æÖÆ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁŹÆäÖĐČúÆ·Ÿ»Ö۔ķ¶Î§ÊÇ[96ŁŹ106]ŁŹŃù±ŸÊęŸĘ·ÖŚéÎȘ[96ŁŹ98Ł©ŁŹ[98ŁŹ100),[100ŁŹ102)ŁŹ[102ŁŹ104),[104ŁŹ106],ÒŃÖȘŃù±ŸÖĐČúÆ·Ÿ»ÖŰĐĄÓÚ100żË”ÄžöÊęÊÇ36ŁŹÔòŃù±ŸÖĐŸ»ÖŰŽóÓÚ»ò”ÈÓÚ98żËČąÇÒĐĄÓÚ104żË”ÄČúÆ·”ÄžöÊęÊÇ( ).
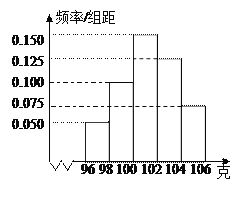
A. 90B. 75C. 60D. 45
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com