
分析 (Ⅰ)求出函数的导数,计算f′(1),f(1)的值,代入切线方程即可;(Ⅱ)问题转化为判断函数g(x)=ex-x-1的单调性,求出g(x)≥0,从而证出结论.
解答 (Ⅰ)解:当m=1时,f(x)=(x2+x+1)ex,
则f′(x)=(x2+3x+2)ex,
∴K=f′(1)=6e,
∵f(1)=3e,
∴曲线y=f(x)在点(1,f(1))处的切线方程为:
y-3e=6e(x-1),即6ex-y-3e=0;
(Ⅱ)证明:由题意,得:
f(x)-(x3+x2+mxex+mex)
=x2ex-x2-x3=x2(ex-x-1),
当x=0时,结论显然成立,
当x>0.∵x2>0,令g(x)=ex-x-1,
则g′(x)=ex-1,
∴当x>0时g(x)为增函数;
当x<0时g(x)为减函数,
∴x=0时g(x)取最小值,g(0)=0.
∴g(x)≥0,∴≥0,
∴f(x)≥x2+x3.
点评 本题考查了曲线的切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在k∈N,使a4k+1>0 | B. | 任给k∈N,使a${\;}_{{2}^{k}}$+1>0 | ||
| C. | 不存在k∈N,使a3k+2<0 | D. | $\sqrt{{a}_{4n+1}{a}_{4n+9}}$=-a4n+5(n∈N) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
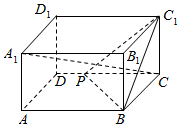 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是棱CD上的一点,DP=λ.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=CC1=1,点P是棱CD上的一点,DP=λ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a$=(1,2),$\overrightarrow b$=(0,0) | B. | $\overrightarrow a$=(1,-2),$\overrightarrow b$=(3,5) | C. | $\overrightarrow a$=(3,2),$\overrightarrow b$=(9,6) | D. | $\overrightarrow a$=(-3,3),$\overrightarrow b$=(2,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,H是球O的直径AB上一点,平面α截球O所得截面的面积为9π,平面α∩AB=H,AH:HB=1:3,且点A到平面α的距离为1,则球O的表面积为40π.
如图,H是球O的直径AB上一点,平面α截球O所得截面的面积为9π,平面α∩AB=H,AH:HB=1:3,且点A到平面α的距离为1,则球O的表面积为40π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com