
分析 化简可得4033-2x=|x-1|+|x-a|+|x-b|,从而讨论以去掉绝对值号,并确定方程的解的个数及条件,从而解得.
解答 解:由方程组消y可得,
4033-2x=|x-1|+|x-a|+|x-b|,
当x≤1时,
4033-2x=1-x-x+a-x+b,
故x=b+a-4032,
故当b+a≤4033时,有一个解;
即a≤4031时,有一个解;否则无解;
当1<x≤a时,
4033-2x=x-1-x+a-x+b,
故x=4034-a-b,
故当-a<4032-a-b≤1,即b<4032且a+b≥4301时,有一个解;
即2015≤a≤4030,有一个解,
否则无解;
当1<x≤b时,
4033-2x=x+a+b-1,
故3x=4034-a-b,
故当3<4034-a-b≤3b,即a+b<4031且a+4b≥4304时,有一个解;
即$\frac{4300}{5}$≤a≤2014,方程有一个解,
否则无解;
当x>b时,
4033-2x=3x+a-b-1,
故5x=4034-a+b,
故当4034-a+b>5b,即a+4b<4304时,有一个解;
否则无解;
综上所述,
当a取最大值4031时,方程有一个解,
故答案为:4031.
点评 本题考查了绝对值方程的解法及分类讨论的思想方法应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
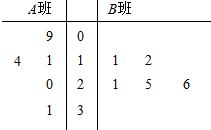 长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 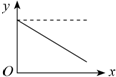 | B. | 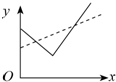 | C. | 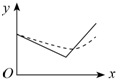 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com