
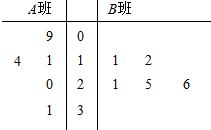
 长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).分析 (Ⅰ)先求出A班样本数据的平均值和B班样本数据的平均值,由此估计B班学生每周平均上网时间较长.
(Ⅱ)A班的样本数据中不超过20的数据a有4个,分别为:9,11,14,20,B班的样本数据中不超过21的数据b有2个,分别为:11,12,由此利用列举法能求出a≤b的概率.
解答 解:(Ⅰ)A班样本数据的平均值为$\frac{1}{5}(9+11+14+20+31)=17$,
由此估计A班学生每周平均上网时间17小时;
B班样本数据的平均值为$\frac{1}{5}(11+12+21+25+26)=19$,
由此估计B班学生每周平均上网时间较长.
(Ⅱ)A班的样本数据中不超过20的数据a有4个,分别为:9,11,14,20
B班的样本数据中不超过21的数据b有2个,分别为:11,12
从A班和B班的样本数据中各随机抽取一个共有:8种不同情况,
分别为:(9,11),(9,12),(11,11),(11,12),(14,11),(14,12),(20,11),(20,12)
其中a≤b的情况有(9,11),(9,12),(11,11),(11,12),共4种,
故a≤b的概率$p=\frac{4}{8}=\frac{1}{2}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -4 | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{18}$ | B. | $\frac{9}{32}$ | C. | $\frac{23}{32}$ | D. | $\frac{17}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com