
分析 (1)通过已知条件代入计算即得结论;
(2)通过${b}_{n+1}=\frac{{b}_{n}}{1-{{a}_{n}}^{2}}$两边同时减1并取倒数,利用an+bn=1化简可知数列{$\frac{1}{{b}_{n}-1}$}是等差数列,进而计算可得结论;
(3)通过(2)可知bn=$\frac{n+2}{n+3}$,进而裂项可知anan+1=$\frac{1}{n+3}$-$\frac{1}{n+4}$,并项相加可知Sn=$\frac{n}{4(n+4)}$,进而问题转化为求$\frac{(n+2)(n+4)}{n(n+3)}$的最小值,计算即得结论.
解答 (1)解:依题意,b1=1-a1=1-$\frac{1}{4}$=$\frac{3}{4}$,
b2=$\frac{{b}_{1}}{1-{{a}_{1}}^{2}}$=$\frac{\frac{3}{4}}{1-\frac{1}{{4}^{2}}}$=$\frac{4}{5}$,a2=1-b2=1-$\frac{4}{5}$=$\frac{1}{5}$,
${b}_{3}=\frac{{b}_{2}}{1-{{a}_{2}}^{2}}$=$\frac{\frac{4}{5}}{1-\frac{1}{{5}^{2}}}$=$\frac{5}{6}$,a3=1-b3=1-$\frac{5}{6}$=$\frac{1}{6}$,
${b}_{4}=\frac{{b}_{3}}{1-{{a}_{3}}^{2}}$=$\frac{\frac{5}{6}}{1-\frac{1}{{6}^{2}}}$=$\frac{6}{7}$;
(2)证明:∵${b}_{n+1}=\frac{{b}_{n}}{1-{{a}_{n}}^{2}}$,an+bn=1,
∴bn+1-1=$\frac{{b}_{n}}{1-{{a}_{n}}^{2}}$-1=$\frac{{b}_{n}}{{b}_{n}+{a}_{n}-{{a}_{n}}^{2}}$-1=$\frac{{{a}_{n}}^{2}-{a}_{n}}{{b}_{n}+{a}_{n}-{{a}_{n}}^{2}}$,
两边同时取倒数,得:$\frac{1}{{b}_{n+1}-1}$=$\frac{{b}_{n}+{a}_{n}-{{a}_{n}}^{2}}{{{a}_{n}}^{2}-{a}_{n}}$
=$\frac{{b}_{n}}{{{a}_{n}}^{2}-{a}_{n}}$-1
=$\frac{{1-a}_{n}}{{a}_{n}({a}_{n}-1)}$-1
=$\frac{1}{-{a}_{n}}$-1
=$\frac{1}{{b}_{n}-1}$-1,
∴数列{$\frac{1}{{b}_{n}-1}$}是等差数列,
又∵$\frac{1}{{b}_{1}-1}$=$\frac{1}{\frac{3}{4}-1}$=-4,
∴$\frac{1}{{b}_{n}-1}$=-4-(n-1)=-(n+3),
∴数列{bn}的通项公式bn=1-$\frac{1}{n+3}$=$\frac{n+2}{n+3}$;
(3)解:由(2)可知bn=$\frac{n+2}{n+3}$,
∴an=1-bn=$\frac{1}{n+3}$,anan+1=$\frac{1}{(n+3)(n+4)}$=$\frac{1}{n+3}$-$\frac{1}{n+4}$,
∴Sn=a1a2+a2a3+…+anan+1
=$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$+…+$\frac{1}{n+3}$-$\frac{1}{n+4}$
=$\frac{1}{4}$-$\frac{1}{n+4}$
=$\frac{n}{4(n+4)}$,
∵不等式4aSn<bn对任意n∈N*恒成立,
∴不等式4a•$\frac{n}{4(n+4)}$<$\frac{n+2}{n+3}$对任意n∈N*恒成立,
∴a<$\frac{(n+2)(n+4)}{n(n+3)}$=1+$\frac{3n+8}{{n}^{2}+3n}$,
∵$\frac{3n+8}{{n}^{2}+3n}$随着n的增大而减小,且$\underset{lim}{n→∞}$$\frac{3n+8}{{n}^{2}+3n}$=0,
∴a≤1.
点评 本题考查数列的通项及前n项和,考查运算求解能力,考查裂项相消法,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
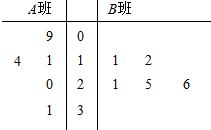 长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某中学为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | ¬p∧q | D. | ¬p∨q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com