
分析 把已知曲线方程变形,然后画出图形,由图形可知,△OAB是直角三角形,包括∠AOB与∠OAB为直角两种情况,然后分类求出a的值,作积得答案.
解答 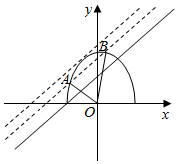 解:由y=$\sqrt{1-2{x}^{2}}$,得2x2+y2=1(y≥0)
解:由y=$\sqrt{1-2{x}^{2}}$,得2x2+y2=1(y≥0)
作出两函数y=x+a与y=$\sqrt{1-2{x}^{2}}$的图象如图,
当OA⊥AB时,OA所在直线方程为y=-x,
联立$\left\{\begin{array}{l}{y=-x}\\{2{x}^{2}+{y}^{2}=1}\end{array}\right.$,解得A(-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$),
把A的坐标代入y=x+a,得a=$\frac{2\sqrt{3}}{3}$;
联立$\left\{\begin{array}{l}{y=x+a}\\{2{x}^{2}+{y}^{2}=1}\end{array}\right.$,得3x2+2ax+a2-1=0.
设A(x1,y1),B(x2,y2),
∴${x}_{1}+{x}_{2}=-\frac{2a}{3}$,${x}_{1}{x}_{2}=\frac{{a}^{2}-1}{3}$,
当OA⊥OB时,-$\frac{{y}_{1}}{{x}_{1}}$•(-$\frac{{y}_{2}}{{x}_{2}}$)=-1,即y1y2=-x1x2,
∴(x1+a)(x2+a)=-x1x2,
则a(x1+x2)+2x1x2+a2=0,
∴-$\frac{2{a}^{2}}{3}$+$\frac{2{a}^{2}-2}{3}$+a2=0,解得a=$\frac{\sqrt{6}}{3}$.
∴满足条件的所有实数a的值的乘积为$\frac{2\sqrt{3}}{3}×\frac{\sqrt{6}}{3}=\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题考查曲线与方程,考查了数形结合的解题思想方法与数学转化思想方法,是中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
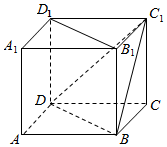 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | a3>b3 | D. | a2>b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com