
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),
第5组[95,100]得到的频率分布直方图如图所示.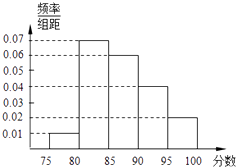
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
【答案】
(1)解:根据所给的频率分步直方图中小正方形的长和宽,
得到第三组的频率为0.06×5=0.3;
第四组的频率为0.04×5=0.2;
第五组的频率为0.02×5=0.1.
(2)解:由题意知本题是一个等可能事件的概率,
由(1)可知第三,四,五组的频率分别为:0.3,0.2,0.1
则分层抽样第3,抽取的人数为: ![]() ×6=3
×6=3
第4组抽取的人数为: ![]() ×6=2
×6=2
5组每组抽取的人数为: ![]() ×6=1;
×6=1;
(3)解:学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,
由题意知变量ξ的可能取值是0,1,2
该变量符合超几何分布,
∴P(ξ=i)= ![]() (i=0,1,2)
(i=0,1,2)
∴ξ分布列是

∴P(ξ≥1)= ![]() +
+ ![]() =
= ![]() =
= ![]()
【解析】(1)根据频率分步直方图的性质,根据所给的频率分步直方图中小矩形的长和宽,求出矩形的面积,即这组数据的频率.(2)由上一问求得频率,可知3,4,5组各自所占的比例样,根据分层抽样的定义进行求解;(3)由题意知变量ξ的可能取值是0,1,2,该变量符合超几何分布,根据超几何分布的概率公式写出变量的概率,写出这组数据的分布列从而求出P(ξ≥1)的概率;


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分10分)设![]() 个正数
个正数![]() 满足
满足![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)当![]() 时,不等式
时,不等式![]() 也成立,请你将其推广到
也成立,请你将其推广到![]() (
(![]() 且
且![]() )个正数
)个正数![]() 的情形,归纳出一般性的结论并用数学归纳法证明.
的情形,归纳出一般性的结论并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在![]() 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线![]() 上.
上.
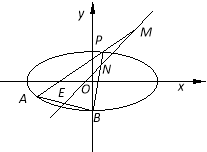
(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线![]() 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2asinωxcosωx+2 ![]() cos2ωx﹣
cos2ωx﹣ ![]() +1(a>0,ω>0)的最大值为3,最小正周期为π.
+1(a>0,ω>0)的最大值为3,最小正周期为π.
(1)求函数f(x)的单调递增区间.
(2)若f(θ)= ![]() ,求sin(4θ+
,求sin(4θ+ ![]() )的值.
)的值.
(3)若存在区间[a,b](a,b∈R,且a<b)使得y=f(x)在[a,b]上至少含有6个零点,在满足上述条件的[a,b]中,求b﹣a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国南宋时期的数学家秦九韶提出的一种多项式f(x)=anxn+an﹣1xn﹣1+…+a1x+a0的求值问题的算法.现按照这个程序执行函数f (x)=3x4﹣2x3﹣6x﹣17的计算,若输入的值x0=2,则输出的v的值是( ) 
A.0
B.2
C.3
D.﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某商业中心O有通往正东方向和北偏东30方向的两条街道,某公园P位于商业中心北偏东![]() 角(
角(![]() ),且与商业中心O的距离为
),且与商业中心O的距离为![]() 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。

(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com