
【题目】(本题满分14分)
如图,在多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
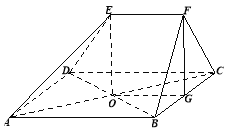
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求证:直线![]()
![]() 平面
平面![]() .
.
【答案】(1)详见解析(2)详见解析
【解析】
试题分析:(1)∵四边形![]() 是菱形,∴点
是菱形,∴点![]() 是
是![]() 的中点,∵点
的中点,∵点![]() 为
为![]() 的中点,由三角形中位线性质得
的中点,由三角形中位线性质得![]() ,再根据线面平行判定定理得直线
,再根据线面平行判定定理得直线![]() 平面
平面![]() .
.
(2)一方面∵四边形![]() 是菱形,∴
是菱形,∴![]() ,另一方面∵
,另一方面∵ ![]() ,点
,点![]() 为
为![]() 的中点, ∴
的中点, ∴![]() ,由面面垂直性质定理得
,由面面垂直性质定理得![]() 平面
平面![]() ,从而
,从而![]() ,又可证四边形
,又可证四边形![]() 为平行四边形,即
为平行四边形,即![]() ,所以
,所以![]() ,最后由线面垂直判定定理得
,最后由线面垂直判定定理得![]() 平面
平面![]() .
.
试题解析:证明(1)∵四边形![]() 是菱形,
是菱形,![]() ,∴点
,∴点![]() 是
是![]() 的中点,
的中点,
∵点![]() 为
为![]() 的中点 ∴
的中点 ∴![]() , 3分
, 3分
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴直线
,∴直线![]() 平面
平面![]() . 7分
. 7分
(2)∵ ![]() ,点
,点![]() 为
为![]() 的中点, ∴
的中点, ∴![]() ,
,
∵平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,
![]() 平面
平面![]() ,
,![]() ∴
∴![]() 平面
平面![]() , 9/span>分
, 9/span>分
∵![]() 平面
平面![]() ∴
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴四边形![]() 为平行四边形, ∴
为平行四边形, ∴![]() , 11分
, 11分
∵![]() ,
,![]() ,∴
,∴![]() , ∵四边形
, ∵四边形![]() 是菱形,∴
是菱形,∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() 在平面
在平面![]() 内,
内,
∴![]() 平面
平面![]() . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年推出一种新型家用轿车,购买时费用为14.4万元,每年应交付保险费、养路费及汽车油费共0.7万元,
汽车维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费用均比上一年增加0.2万元
(1)设该辆轿车使用n年的总费用(包括购买费用,保险费,养路费,汽车费及维修费)为f(n),求f(n)的表达式.
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),
第5组[95,100]得到的频率分布直方图如图所示.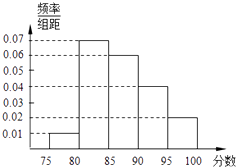
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD= ![]() ,E是BC中点,点Q在侧棱PC上.
,E是BC中点,点Q在侧棱PC上. 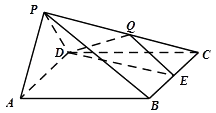
(1)求证:AD⊥PB;
(2)若Q是PC中点,求二面角E﹣DQ﹣C的余弦值;
(3)若 ![]() ,当PA∥平面DEQ时,求λ的值.
,当PA∥平面DEQ时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位“准笑星”在“信阳笑星”选拔赛中,5位评委给出的评分情况如图所示,记甲、乙两人的平均得分分别为 ![]() 、
、 ![]() ,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
A.![]() <
< ![]() ,s1<s2
,s1<s2
B.![]() <
< ![]() ,s1>s2
,s1>s2
C.![]() >
> ![]() ,s1<s2
,s1<s2
D.![]() >
> ![]() ,s1>s2
,s1>s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有红、黄、蓝三种颜色小旗各2面,将他们排成3行2列,要求每行及每列的颜色均互不相同,则不同的排列方法共有( )
A. 12种 B. 18种 C. 24种 D. 36种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com