
����Ŀ��2014���Ƴ�һ�����ͼ��ýγ�������ʱ����Ϊ14.4��Ԫ��ÿ��Ӧ�������շѡ���·�Ѽ������ͷѹ�0.7��Ԫ��
����ά��Ϊ����һ����ά���ã��ڶ���Ϊ0.2��Ԫ���ӵ�������ÿ���ά���þ�����һ������0.2��Ԫ
��1��������γ�ʹ��n����ܷ��ã�����������ã����շѣ���·�ѣ������Ѽ�ά�ѣ�Ϊf��n������f��n���ı���ʽ��
��2����������ʹ�ö����걨������㣨���ó�ʹ�ö����꣬��ƽ���������٣���
���𰸡�
��1���⣺������ã�ÿ���ά�ѹ���һ�Ȳ����У�n���ά���ܷ���Ϊ
![]() ����Ԫ��
����Ԫ��
����f��n��=14.4+0.7n+��0.1n2��0.1n��
=0.1n2+0.6n+14.4����Ԫ��
��2���⣺�����γ�ʹ��n�����ƽ������Ϊ
![]()
0.1n+0.6+ ![]()
![]()
=3����Ԫ��
���ҽ��� ![]() ʱȡ�Ⱥţ���ʱn=12
ʱȡ�Ⱥţ���ʱn=12
����������ʹ��12�걨�������
����������1������֪��ij����������ʱ����Ϊ14.4��Ԫ��ÿ��Ӧ�������շѡ���·�Ѽ����ͷѹ�0.7��Ԫ��������ά��Ϊ����һ��0.2��Ԫ���ڶ���0.4��Ԫ��������0.6��Ԫ���������Ȳ�����������������ݵȲ�����ǰn���ʽ�����ɵõ�f��n���ı���ʽ����2���ɣ�1����ʹ��n��ó����ܷ��ã��õ�n��ƽ�����ñ���ʽ�����ݻ�������ʽ�������ƽ��������Сʱ��nֵ�������õ����ۣ�


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��a|��
��1����f��x����m�Ľ⼯Ϊ{x|��1��x��5}����ʵ��a��m��ֵ��
��2����a=2��0��t��2ʱ�������x�IJ���ʽf��x��+t��f��x+2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() =��cos2x��
=��cos2x�� ![]() sinx����
sinx���� ![]() =��1��cosx��������f��x��=2
=��1��cosx��������f��x��=2 ![]()
![]() +m���ҵ�x��[0��
+m���ҵ�x��[0�� ![]() ]ʱ��f��x������СֵΪ2��
]ʱ��f��x������СֵΪ2��
��1����m��ֵ������f��x��ͼ��ĶԳ��᷽�̣�
��2���躯��g��x��=[f��x��2]��f��x����x��[0�� ![]() ]����g��x�������ֵ��
]����g��x�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ֱ�������ε����߶�����ͬ���ij��ȣ�������µ������ε���״Ϊ�� ��
A.���������
B.ֱ��������
C.�۽�������
D.�����ӵij��Ⱦ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Բ![]() ����B�����¶��㣬����B��ֱ�߽���ԲC����һ��A��A����
����B�����¶��㣬����B��ֱ�߽���ԲC����һ��A��A����![]() ���·��������߶�AB���е�E��ֱ��
���·��������߶�AB���е�E��ֱ��![]() ��.
��.
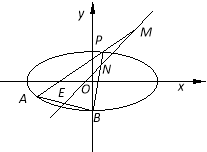
��1����ֱ��AB�ķ��̣�
��2������PΪ��ԲC������A��B�Ķ��㣬��ֱ��AP,BP�ֱ�ֱ��![]() �ڵ�M��N��֤����OM��ONΪ��ֵ.
�ڵ�M��N��֤����OM��ONΪ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������16�֣���֪����![]() ��
�� ![]() ��
��
��1��������![]() ��
��![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ֱ��![]() �Ǻ���
�Ǻ���![]() ͼ������ߣ���
ͼ������ߣ���![]() ����Сֵ��
����Сֵ��
��3����![]() ʱ����
ʱ����![]() ��
��![]() ��ͼ������������
��ͼ������������![]() ����֤��
����֤�� ![]()
![]() ����ȡ
����ȡ![]() Ϊ
Ϊ![]() ��ȡ
��ȡ![]() Ϊ
Ϊ![]() ��ȡ
��ȡ![]() Ϊ
Ϊ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2asin��xcos��x+2 ![]() cos2��x��
cos2��x�� ![]() +1��a��0���أ�0�������ֵΪ3����С������Ϊ�У�
+1��a��0���أ�0�������ֵΪ3����С������Ϊ�У�
��1������f��x���ĵ����������䣮
��2����f���ȣ�= ![]() ����sin��4��+
����sin��4��+ ![]() ����ֵ��
����ֵ��
��3������������[a��b]��a��b��R����a��b��ʹ��y=f��x����[a��b]�����ٺ���6����㣬����������������[a��b]�У���b��a����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������14����
��ͼ���ڶ�����![]() �У��ı���
�У��ı���![]() �����Σ�
�����Σ�![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() ��ƽ��
��ƽ��![]()
![]() ƽ��
ƽ��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
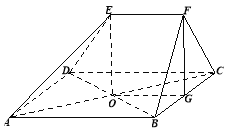
��1����֤��ֱ��![]() ƽ��
ƽ��![]() ��
��
��2����֤��ֱ��![]()
![]() ƽ��
ƽ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�Ա߷ֱ�Ϊa��b��c��sinA+sinB=2sinC��a=2b��
��1��֤������ABCΪ�۽������Σ�
��2����S��ABC= ![]()
![]() ����c��
����c��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com