
【题目】已知函数f(x)=2asinωxcosωx+2 ![]() cos2ωx﹣
cos2ωx﹣ ![]() +1(a>0,ω>0)的最大值为3,最小正周期为π.
+1(a>0,ω>0)的最大值为3,最小正周期为π.
(1)求函数f(x)的单调递增区间.
(2)若f(θ)= ![]() ,求sin(4θ+
,求sin(4θ+ ![]() )的值.
)的值.
(3)若存在区间[a,b](a,b∈R,且a<b)使得y=f(x)在[a,b]上至少含有6个零点,在满足上述条件的[a,b]中,求b﹣a的最小值.
【答案】
(1)解:f(x)=2asinωxcosωx+2 ![]() cos2ωx﹣
cos2ωx﹣ ![]() +1=asin2ωx+
+1=asin2ωx+ ![]() cos2ωx+1=
cos2ωx+1= ![]() sin(2ωx+φ)+1,
sin(2ωx+φ)+1,
∵f(x)的最大值为3,最小正周期为π.
∴ ![]() +1=3,
+1=3, ![]() =π,a>0,ω>0.
=π,a>0,ω>0.
解得a=1,ω=1.
∴f(x)=2sin ![]() +1.
+1.
令2kπ- ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
解得 ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
可得函数f(x)的单调增区间为 ![]() ,k∈Z.
,k∈Z.
(2)解:∵f(θ)= ![]() ,
,
∴2sin ![]() =
= ![]() ,即sin
,即sin ![]() =
= ![]() ,
,
∴sin(4θ+ ![]() )=sin
)=sin ![]() =﹣cos
=﹣cos ![]() =
= ![]() ﹣1=2×
﹣1=2× ![]() ﹣1=﹣
﹣1=﹣ ![]() .
.
(3)解:令f(x)=0,可得sin ![]() =﹣
=﹣ ![]() ,∴x=k
,∴x=k ![]() ,或x=kπ﹣
,或x=kπ﹣ ![]() ,
,
故相邻的零点之间的间隔依次为 ![]() ,
, ![]() .
.
y=f(x)在[a,b]上至少含有6个零点,等价于b﹣a的最小值为 ![]() +3×
+3× ![]() =
= ![]()
【解析】(1)利用倍角公式与和差公式可得:f(x)= ![]() sin(2ωx+φ)+1,根据f(x)的最大值为3,最小正周期为π.可得
sin(2ωx+φ)+1,根据f(x)的最大值为3,最小正周期为π.可得 ![]() +1=3,
+1=3, ![]() =π,a>0,ω>0.即可得出.再利用正弦函数的单调性即可得出单调区间.(2)由f(θ)=
=π,a>0,ω>0.即可得出.再利用正弦函数的单调性即可得出单调区间.(2)由f(θ)= ![]() ,可得sin
,可得sin ![]() =
= ![]() ,利用诱导公式与倍角公式即可得出.(3)令f(x)=0,可得sin
,利用诱导公式与倍角公式即可得出.(3)令f(x)=0,可得sin ![]() =﹣
=﹣ ![]() ,x=k
,x=k ![]() ,或x=kπ﹣
,或x=kπ﹣ ![]() ,故相邻的零点之间的间隔依次为
,故相邻的零点之间的间隔依次为 ![]() ,
, ![]() .即可得出.
.即可得出.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为正方形,AA1=2AB,E为AA1的中点,则异面直线BE与CD1所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年推出一种新型家用轿车,购买时费用为14.4万元,每年应交付保险费、养路费及汽车油费共0.7万元,
汽车维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费用均比上一年增加0.2万元
(1)设该辆轿车使用n年的总费用(包括购买费用,保险费,养路费,汽车费及维修费)为f(n),求f(n)的表达式.
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)如图,在平面直角坐标系![]() 中,离心率为
中,离心率为![]() 的椭圆
的椭圆![]()
![]() 的左顶点为
的左顶点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点.若直线
两点.若直线![]() 斜率为
斜率为![]() 时,
时, ![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试问以![]() 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线![]() 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),
第5组[95,100]得到的频率分布直方图如图所示.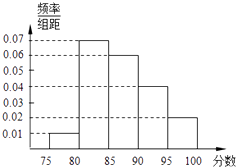
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位“准笑星”在“信阳笑星”选拔赛中,5位评委给出的评分情况如图所示,记甲、乙两人的平均得分分别为 ![]() 、
、 ![]() ,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
A.![]() <
< ![]() ,s1<s2
,s1<s2
B.![]() <
< ![]() ,s1>s2
,s1>s2
C.![]() >
> ![]() ,s1<s2
,s1<s2
D.![]() >
> ![]() ,s1>s2
,s1>s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶120千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时12元.
升,司机的工资是每小时12元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com