
【题目】(本题满分16分)如图,在平面直角坐标系![]() 中,离心率为
中,离心率为![]() 的椭圆
的椭圆![]()
![]() 的左顶点为
的左顶点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点.若直线
两点.若直线![]() 斜率为
斜率为![]() 时,
时, ![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试问以![]() 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线![]() 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
【答案】(1)![]() (2)过定点
(2)过定点![]() .
.
【解析】试题分析:(1)因为离心率为![]() ,所以要确定椭圆标准方程,只需再确定一个独立条件,即点P坐标:根据点
,所以要确定椭圆标准方程,只需再确定一个独立条件,即点P坐标:根据点![]() 斜率为
斜率为![]() 且
且![]() 可求
可求![]() ,所以
,所以![]() ,又
,又![]() ,解得椭圆
,解得椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)用点P坐标表示出![]() 的坐标及以
的坐标及以![]() 为直径的圆的方程:设
为直径的圆的方程:设![]() ,则直线
,则直线![]() 方程为:
方程为: ![]() ,∴
,∴ ,直线
,直线![]() 方程为:
方程为: ![]() ,∴
,∴ ,以
,以![]() 为直径的圆为
为直径的圆为 ,利用
,利用![]() 化简得
化简得![]() ,所以动圆必过
,所以动圆必过![]() 与
与![]() 的交点
的交点![]()
试题解析:解:(1)设 ,
,
∵直线![]() 斜率为
斜率为![]() 时,
时, ![]() ,∴
,∴ ,∴
,∴![]() 3分
3分
∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() . 6分
. 6分
(2)以![]() 为直径的圆过定点
为直径的圆过定点![]() .
.
设![]() ,则
,则![]() ,且
,且![]() ,即
,即![]() ,
,
∵![]() ,∴直线
,∴直线![]() 方程为:
方程为: ![]() ,∴
,∴ ,
,
直线![]() 方程为:
方程为: ![]() ,∴
,∴ , 9分
, 9分
以![]() 为直径的圆为
为直径的圆为
即![]() , 12分
, 12分
∵![]() ,∴
,∴![]() ,
,
令![]() ,
,![]() ,解得
,解得![]() ,
,
∴以![]() 为直径的圆过定点
为直径的圆过定点![]() . 16分
. 16分


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分为16分)设A,B分别为椭圆![]()
![]() 的左、右顶点,椭圆的长轴长为
的左、右顶点,椭圆的长轴长为![]() ,且点
,且点![]() 在该椭圆上.
在该椭圆上.
(1)求椭圆的方程;
(2)设![]() 为直线
为直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 与椭圆相交于异于
与椭圆相交于异于![]() 的点
的点![]() ,证明:△
,证明:△![]() 为钝角三角形.
为钝角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号001,002,…,699,700.从中抽取70个样本,如图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第5个样本编号是( ) 
A.607
B.328
C.253
D.007
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在![]() 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线![]() 上.
上.
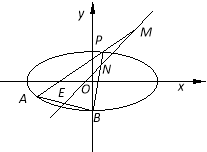
(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线![]() 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)数列![]() ,
, ![]() ,
, ![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() .
.
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() ,
, ![]() 都是等差数列,求证:数列
都是等差数列,求证:数列![]() 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列![]() 是等差数列,试判断当
是等差数列,试判断当![]() 时,数列
时,数列![]() 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2asinωxcosωx+2 ![]() cos2ωx﹣
cos2ωx﹣ ![]() +1(a>0,ω>0)的最大值为3,最小正周期为π.
+1(a>0,ω>0)的最大值为3,最小正周期为π.
(1)求函数f(x)的单调递增区间.
(2)若f(θ)= ![]() ,求sin(4θ+
,求sin(4θ+ ![]() )的值.
)的值.
(3)若存在区间[a,b](a,b∈R,且a<b)使得y=f(x)在[a,b]上至少含有6个零点,在满足上述条件的[a,b]中,求b﹣a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国南宋时期的数学家秦九韶提出的一种多项式f(x)=anxn+an﹣1xn﹣1+…+a1x+a0的求值问题的算法.现按照这个程序执行函数f (x)=3x4﹣2x3﹣6x﹣17的计算,若输入的值x0=2,则输出的v的值是( ) 
A.0
B.2
C.3
D.﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com