
【题目】如图,某商业中心O有通往正东方向和北偏东30方向的两条街道,某公园P位于商业中心北偏东![]() 角(
角(![]() ),且与商业中心O的距离为
),且与商业中心O的距离为![]() 公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。
公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处。

(1)当AB沿正北方向时,试求商业中心到A,B两处的距离和;
(2)若要使商业中心O到A,B两处的距离和最短,请确定A,B的最佳位置。
【答案】(1)13.5km.(2)商业中心到A、B两处的距离和最短为9km,此时OA=6km,OB=3km
【解析】试题分析:(1)建立直角坐标系表示图中各量关系是解题关键: ![]() ,OB=2OA=9,商业中心到A、B两处的距离和为13.5km.(2)当AB与
,OB=2OA=9,商业中心到A、B两处的距离和为13.5km.(2)当AB与![]() 轴不垂直时,设AB:
轴不垂直时,设AB: ![]() ,则
,则![]() ,又直线OB的方程为
,又直线OB的方程为![]() ,所以
,所以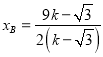 ,
, ![]() ,从而
,从而![]() ,其中
,其中![]() ,或
,或![]() .利用导数可得当
.利用导数可得当![]() 时,
时, ![]() 有极小值也是最小值为9km;此时OA=6km,OB=3km,
有极小值也是最小值为9km;此时OA=6km,OB=3km,
试题解析:

(1)以O为原点,OA所在直线为![]() 轴建立坐标系.设
轴建立坐标系.设![]() ,
,
∵![]() ,
, ![]() ∴
∴![]() ,
, ![]() ,
,
则![]() ,
, ![]() , 4分
, 4分
依题意,AB⊥OA,则OA=![]() ,OB=2OA=9,商业中心到A、B两处的距离和为13.5km. 7分
,OB=2OA=9,商业中心到A、B两处的距离和为13.5km. 7分
(2)
方法1:当AB与![]() 轴不垂直时,设AB:
轴不垂直时,设AB: ![]() ,①
,①
令![]() ,得
,得![]() ;由题意,直线OB的方程为
;由题意,直线OB的方程为![]() ,②
,②
解①②联立的方程组,得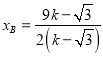 ,∴
,∴![]() ,
,
∴![]() ,由
,由![]() ,
, ![]() ,得
,得![]() ,或
,或![]() . 11分
. 11分
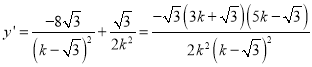 ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 是减函数;当
是减函数;当![]() 时,
时, ![]() ,
, ![]() 是增函数,
是增函数,
∴当![]() 时,
时, ![]() 有极小值为9km;当
有极小值为9km;当![]() 时,
时, ![]() ,
, ![]() 是减函数,结合(1)知
是减函数,结合(1)知![]() km.
km.
综上所述,商业中心到A、B两处的距离和最短为9km,此时OA=6km,OB=3km,
方法2:如图,过P作PM//OA交OB于M,PN//OB交OA于N,设∠BAO= ![]() ,
,
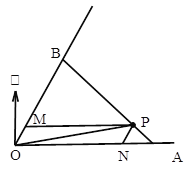
△OPN中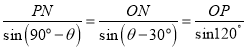 ,得PN=1,ON=4=PM,
,得PN=1,ON=4=PM,
△PNA中∠NPA=120°- ![]() ∴
∴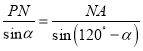 得
得![]()
同理在△PMB中, 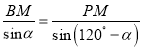 ,得
,得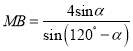 ,
,
 , 13分
, 13分
当且仅当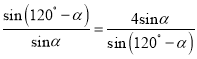 即
即![]() 即
即![]() 时取等号.
时取等号.
方法3:若设点![]() ,则AB:
,则AB: 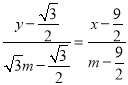 ,得
,得![]() ,
,
∴![]() , 13分
, 13分
当且仅当![]() 即
即![]() 时取等号.
时取等号.
方法4:设![]() ,AB:
,AB:  ,得
,得![]() ,
,
![]() , 13分
, 13分
当且仅当![]() 即
即![]() 时取等号.
时取等号.
答:A选地址离商业中心6km,B离商业中心3km为最佳位置. 15分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),
第5组[95,100]得到的频率分布直方图如图所示.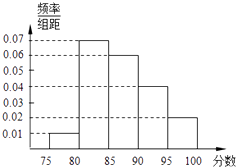
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位“准笑星”在“信阳笑星”选拔赛中,5位评委给出的评分情况如图所示,记甲、乙两人的平均得分分别为 ![]() 、
、 ![]() ,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
A.![]() <
< ![]() ,s1<s2
,s1<s2
B.![]() <
< ![]() ,s1>s2
,s1>s2
C.![]() >
> ![]() ,s1<s2
,s1<s2
D.![]() >
> ![]() ,s1>s2
,s1>s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图像如图所示,则下列结论中一定成立的是( ) 
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(﹣2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(﹣2)
D.函数f(x)有极大值f(﹣2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1,F2分别是椭圆![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
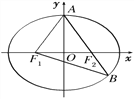
(Ⅰ)求椭圆C的离心率;
(Ⅱ)已知△AF1B的面积为![]() ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶120千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时12元.
升,司机的工资是每小时12元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax2+bx+c图像上的点P(1,f(1))处的切线方程为y=﹣3x+1.
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式;
(2)函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com