
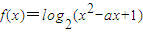 的值域为R,则-2<a<2;
的值域为R,则-2<a<2;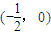 对称;
对称;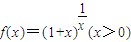 ,则存在无数多个正实数M,使得|f(x)|≤M成立;
,则存在无数多个正实数M,使得|f(x)|≤M成立; 的图象,从图象上观察可知.
的图象,从图象上观察可知. 解:由于函数y=sin|x|不是周期函数,故排除①.
解:由于函数y=sin|x|不是周期函数,故排除①.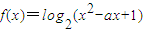 的值域为R,则对于二次函数y=x2-ax+1,应有△=a2-4>0,解得 a<-2,或 a>2,故排除②.
的值域为R,则对于二次函数y=x2-ax+1,应有△=a2-4>0,解得 a<-2,或 a>2,故排除②.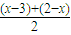 =-
=- ,故f(x)的图象关于点(1,0)对称,故③正确.
,故f(x)的图象关于点(1,0)对称,故③正确.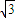 x,故表示的图形是两条相交直线,故④正确.
x,故表示的图形是两条相交直线,故④正确.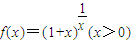 的图象上观察可知,当x>0时,其最大值不超过3,
的图象上观察可知,当x>0时,其最大值不超过3,

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
| π |
| 3 |
| 5π |
| 12 |
| ||
| 2 |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| π |
| 2 |
| 5π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| π |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com