
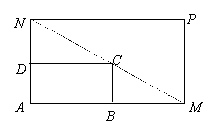
如图所示 ,
,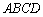 是一个矩形花坛,其中
是一个矩形花坛,其中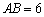 米,
米,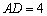 米.现将矩形花坛
米.现将矩形花坛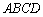 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛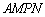 ,要求:
,要求: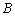 在
在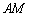 上,
上,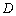 在
在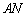 上,对角线
上,对角线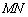 过
过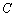 点,且矩形
点,且矩形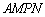 的面积小于150平方米.
的面积小于150平方米.
(1)设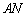 长为
长为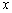 米,矩形
米,矩形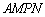 的面积为
的面积为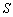 平方米,试用解析式将
平方米,试用解析式将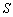 表示成
表示成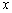 的函数,并确定函数的定义域;
的函数,并确定函数的定义域;
(2)当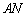 的长度是多少时,矩形
的长度是多少时,矩形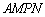 的面积最小?并求最小面积.
的面积最小?并求最小面积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知曲线C:xy=1,过C上一点An(xn,yn)作一斜率为kn=-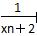 的直线交曲线C于另一点An+1(xn+1,yn+1),点列{An}的横坐标构成数列{xn},其中x1=
的直线交曲线C于另一点An+1(xn+1,yn+1),点列{An}的横坐标构成数列{xn},其中x1=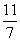 .
.
(1)求xn与xn+1的关系式;
(2)令bn=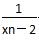 +
+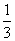 ,求证:数列{bn}是等比数列;
,求证:数列{bn}是等比数列;
(3)若cn=3n-λbn(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有cn+1>cn成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
某校高三年级学生会主席团有共有5名同学组成,其中有3名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
|
| A. | 0.35 | B. | 0.4 | C. | 0.6 | D. | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数 f(x)=﹣x+2,x∈[﹣5,5]若从区间[﹣5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
f(x)=﹣x+2,x∈[﹣5,5]若从区间[﹣5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
|
| A. | 0.5 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某生产厂商更新设备,已知在未来x 年内,此设备所花费的各种费用总和y(万元)与x
满足函数关系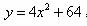 ,若欲使此设备的年平均花费最低,则此设备的使用年限x为
,若欲使此设备的年平均花费最低,则此设备的使用年限x为
( )
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com