
【题目】如图,C、D是以AB为直径的圆上两点,AB=2AD=2 ![]() ,AC=BC,F 是AB上一点,且AF=
,AC=BC,F 是AB上一点,且AF= ![]() AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE= ![]() .
. 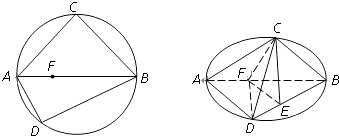
(1)求证:AD⊥平面BCE;
(2)求证:AD∥平面CEF;
(3)求三棱锥A﹣CFD的体积.
【答案】
(1)证明:依题AD⊥BD,
∵CE⊥平面ABD,∴CE⊥AD,
∵BD∩CE=E,
∴AD⊥平面BCE
(2)证明:Rt△BCE中,CE= ![]() ,BC=
,BC= ![]() ,∴BE=2,
,∴BE=2,
Rt△ABD中,AB=2 ![]() ,AD=
,AD= ![]() ,∴BD=3.
,∴BD=3.
∴ ![]() .
.
∴AD∥EF,∵AD在平面CEF外,
∴AD∥平面CEF
(3)解:由(2)知AD∥EF,AD⊥ED,
且ED=BD﹣BE=1,
∴F到AD的距离等于E到AD的距离为1.
∴S△FAD= ![]() =
= ![]() .
.
∵CE⊥平面ABD,
∴VA﹣CFD=VC﹣AFD= ![]() =
= ![]() =
= ![]()
【解析】(1)依题AD⊥BD,CE⊥AD,由此能证明AD⊥平面BCE.(2)由已知得BE=2,BD=3.从而AD∥EF,由此能证明AD∥平面CEF.(3)由VA﹣CFD=VC﹣AFD,利用等积法能求出三棱锥A﹣CFD的体积.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】某颜料公司生产![]() 、
、![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,生产每吨
吨,生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过
吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过![]() 吨、
吨、![]() 吨、
吨、![]() 吨,如果
吨,如果![]() 产品的利润为
产品的利润为![]() 元/吨,
元/吨, ![]() 产品的利润为
产品的利润为![]() 元/吨,则该颜料公司一天内可获得的最大利润为( )
元/吨,则该颜料公司一天内可获得的最大利润为( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x﹣30°)+cos(x﹣60°),g(x)=2sin2 ![]() .
.
(1)若α为第一象限角且f(α)= ![]() ,求g(α)之值;
,求g(α)之值;
(2)求f(x﹣1080°)≥g(x)在[0,360°]内的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C为圆心的圆经过点A(﹣1,0)和B(3,4),且圆心在直线x+3y﹣15=0上.
(1)求圆C的方程;
(2)设点P在圆C上,求△PAB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设P是圆![]() 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且![]() ,
,
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为![]() 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.
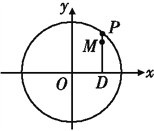
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图半圆柱![]() 的底面半径和高都是1,面
的底面半径和高都是1,面![]() 是它的轴截面(过上下底面圆心连线
是它的轴截面(过上下底面圆心连线![]() 的平面),
的平面),![]() 分别是上下底面半圆周上一点.
分别是上下底面半圆周上一点.
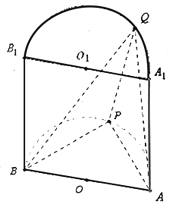
(1)证明:三棱锥![]() 体积
体积![]() ,并指出
,并指出![]() 和
和![]() 满足什么条件时有
满足什么条件时有![]()
(2)求二面角![]() 平面角的取值范围,并说明理由.
平面角的取值范围,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图: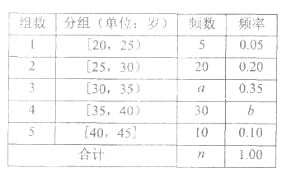
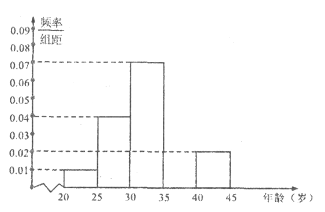
(1)求出表中的![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在![]() 的选取2名担任主要发言人.记这2名主要发言人年龄在
的选取2名担任主要发言人.记这2名主要发言人年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com