练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知以点C为圆心的圆经过点A（﹣1，0）和B（3，4），且圆心在直线x+3y﹣15=0上．
    （1）求圆C的方程；
    （2）设点P在圆C上，求△PAB的面积的最大值．

    【答案】
    （1）解：依题意，所求圆的圆心C为AB的垂直平分线和直线x+3y﹣15=0的交点，

    ∵AB中点为（1，2）斜率为1，

    ∴AB垂直平分线方程为y﹣2=（x﹣1）即y=﹣x+3

    联立 ，解得 ，即圆心（﹣3，6），

    半径

    ∴所求圆方程为（x+3）2+（y﹣6）2=40


    （2）解： ，

    圆心到AB的距离为

    ∵P到AB距离的最大值为

    ∴△PAB面积的最大值为


    【解析】（1）依题意，所求圆的圆心C为AB的垂直平分线和直线x+3y﹣15=0的交点，求出圆心与半径，即可求圆C的方程；（2）求出|AB|，圆心到AB的距离d，求出P到AB距离的最大值d+r，即可求△PAB的面积的最大值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】是指大气中直径小于或等于微米的颗粒物，也称为可入肺颗粒物，对人体健康和大气环境质量的影响很大.我国标准采用世卫组织设定的最宽限值.即日均值在35微克/立方米以下空气质量为一级；在35微克/立方米75微克/立方米之间空气质量为二级；75微克/立方米以上空气质量为超标.

    某市环保局从360天的市区监测数据中统计了1月至10月的每月的平均值（单位：微克/立方米），如下表所示.

    月份

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    月均值

    32

    28

    25

    31

    34

    33

    45

    44

    63

    68

    （1）从5月到10月的这6个数据中任取2个数值，求这个2个数值均为二级的概率；

    （2）求月均值关于月份的回归直线方程，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在△ABC中，A=450，AB=，BC=2，求解此三角形.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

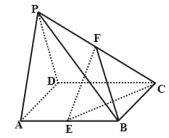
    【题目】如图所示，在四棱锥中，底面是边长为2的正方形，侧面为正三角形，且面面， 分别为棱的中点.

    （1）求证： 平面；

    （2）（文科）求三棱锥的体积；

    （理科）求二面角的正切值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆过两点， ，且圆心在直线上.

    （1）求圆的标准方程；

    （2）直线过点且与圆有两个不同的交点，若直线的斜率大于0，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ，g（x）=x2+2mx+
    （1）用定义法证明f（x）在R上是增函数；
    （2）求出所有满足不等式f（2a﹣a2）+f（3）＞0的实数a构成的集合；
    （3）对任意的实数x1∈[﹣1，1]，都存在一个实数x2∈[﹣1，1]，使得f（x1）=g（x2），求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，C、D是以AB为直径的圆上两点，AB=2AD=2 ，AC=BC，F 是AB上一点，且AF= AB，将圆沿直径AB折起，使点C在平面ABD的射影E在BD上，已知CE= ．

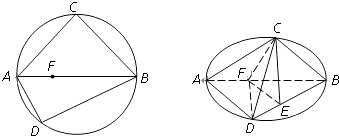
    （1）求证：AD⊥平面BCE；
    （2）求证：AD∥平面CEF；
    （3）求三棱锥A﹣CFD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知矩形四点坐标为A（0，-2），C（4，2），B（4，-2），D（0，2）．

    （1）求对角线所在直线的方程；

    （2）求矩形外接圆的方程；

    （3）若动点为外接圆上一点，点为定点，问线段PN中点的轨迹是什么，并求出该轨迹方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项均为正数的等比数列{an}中，a2=4，a4=16．
    （1）求公比q；
    （2）若a3 ， a5分别为等差数列{bn}的第3项和第5项，求数列{bn}的通项公式．

    查看答案和解析>>

    同步练习册答案