
【题目】已知在△ABC中,A=450,AB=![]() ,BC=2,求解此三角形.
,BC=2,求解此三角形.
【答案】B=75°, C=60°, AC=![]() 或C=120°, B=15°,AC=
或C=120°, B=15°,AC=![]()
【解析】试题分析:方法一:先由正弦定理求得![]() 或
或![]() ,再用三角形内角和定理求得
,再用三角形内角和定理求得![]() ,最后用正弦定理求
,最后用正弦定理求![]() 。
。
方法二:先由余弦定理求得![]() ,再用正弦定理求得
,再用正弦定理求得![]() 或
或![]() ,最后用三角形内角和定理求
,最后用三角形内角和定理求![]() 。
。
试题解析:方法一:
在△ABC中,A=45°,![]() ,BC=2,
,BC=2,
由正弦定理得![]() ,
,
∴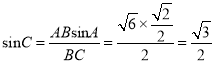 ,
,
又![]() ,所以
,所以![]() 。
。
∴![]() 或
或![]() 。
。
①当![]() 时,
时, ![]() ,
,
由正弦定理得![]() ,
,
∴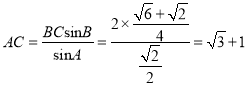 。
。
②当![]() 时,
时, ![]()
由正弦定理得![]() ,
,
∴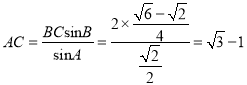 。
。
综上![]() 或
或![]() 。
。
方法二:
由余弦定理:BC2=AC2+AB2﹣2ABACcos∠A
∴![]() ,
,
整理得 ![]() ,
,
解得:AC=![]() 或AC=
或AC=![]() .
.
∴![]() ,BC=2,AC=
,BC=2,AC=![]() 或AC=
或AC=![]() ,
,![]() ,BC=2,
,BC=2,
在△ABC中由正弦定理得![]() ,
,
可得:sinC=![]() ,
,
∵A=45°,A+B+C=180°
∴0<C<135°
当C=60°时,则B=180°﹣45°﹣60°=75°.
当C=120°时,则B=180°﹣45°﹣120°=15°.
综上![]() 或
或![]() 。
。


科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]()
![]() ,其中向量
,其中向量 ![]() =(2cosx,1),
=(2cosx,1), ![]() =(cosx,
=(cosx, ![]() sin2x),x∈R.
sin2x),x∈R.
(1)求f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知f(A)=2,b=1,△ABC的面积为 ![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产![]() 、
、![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,生产每吨
吨,生产每吨![]() 产品,需要甲染料
产品,需要甲染料![]() 吨,乙染料
吨,乙染料![]() 吨,丙染料
吨,丙染料![]() 吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过
吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过![]() 吨、
吨、![]() 吨、
吨、![]() 吨,如果
吨,如果![]() 产品的利润为
产品的利润为![]() 元/吨,
元/吨, ![]() 产品的利润为
产品的利润为![]() 元/吨,则该颜料公司一天内可获得的最大利润为( )
元/吨,则该颜料公司一天内可获得的最大利润为( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱A1B1C1 - ABC中,侧棱AA1丄底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是

A. CC1与B1E是异面直线 B. AC丄平面ABB1A1
C. A1C1∥平面AB1E D. AE与B1C1为异面直线,且AE丄B1C1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考山东理数】平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的离心率是
的离心率是![]() ,抛物线E:
,抛物线E:![]() 的焦点F是C的一个顶点.
的焦点F是C的一个顶点.
(I)求椭圆C的方程;
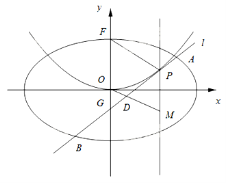
(II)设P是E上的动点,且位于第一象限,E在点P处的切线![]() 与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
(i)求证:点M在定直线上;
(ii)直线![]() 与y轴交于点G,记
与y轴交于点G,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=sin(x﹣30°)+cos(x﹣60°),g(x)=2sin2 ![]() .
.
(1)若α为第一象限角且f(α)= ![]() ,求g(α)之值;
,求g(α)之值;
(2)求f(x﹣1080°)≥g(x)在[0,360°]内的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C为圆心的圆经过点A(﹣1,0)和B(3,4),且圆心在直线x+3y﹣15=0上.
(1)求圆C的方程;
(2)设点P在圆C上,求△PAB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取![]() 名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图:
名市民,按年龄情况进行统计的频率分布表和频率分布直方图如图: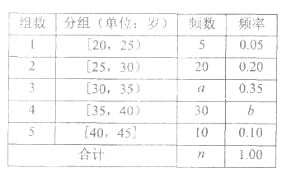
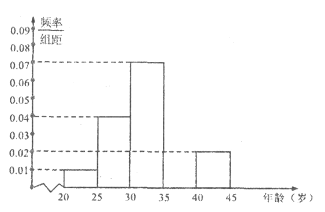
(1)求出表中的![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在![]() 的选取2名担任主要发言人.记这2名主要发言人年龄在
的选取2名担任主要发言人.记这2名主要发言人年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com