
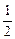 成等比数列
成等比数列
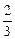 ,a3=-
,a3=-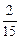 ,a4=-
,a4=-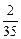 ,由此可推出
,由此可推出 an=
an=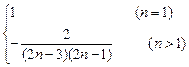
 ∵an,Sn,Sn-
∵an,Sn,Sn-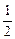 成等比数列,
成等比数列,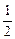 )(n≥2) (*)
)(n≥2) (*)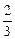
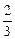 ,S3=
,S3=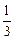 +a3代入(*)式得
+a3代入(*)式得 a3=-
a3=-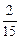
 a4=-
a4=-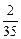 ,由此可推出
,由此可推出 an=
an=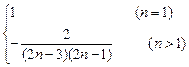

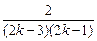 成立
成立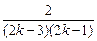 ·(Sk-
·(Sk-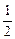 )
)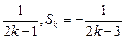 (舍)
(舍)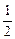 ),得(Sk+ak+1)2=ak+1(ak+1+Sk-
),得(Sk+ak+1)2=ak+1(ak+1+Sk-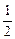 )
)
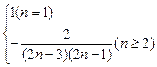 对一切n∈N成立
对一切n∈N成立


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
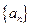 的各项均为正数,观察下面程序框图,
的各项均为正数,观察下面程序框图,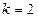 ;
;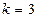 时,
时,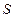 的表达式。
的表达式。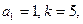 时,有
时,有 ,求数列
,求数列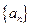 的通项公式
的通项公式 ;
;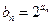 ,求
,求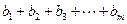 的
的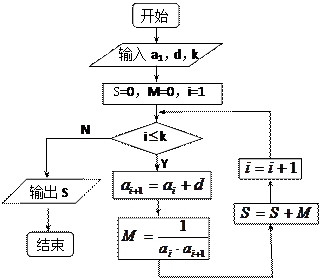
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
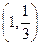 是函数
是函数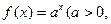 且
且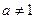 )的图象上一点,等比数列
)的图象上一点,等比数列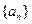 的前
的前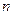 项和为
项和为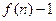 ,数列
,数列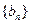
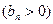 的首项为
的首项为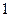 ,且前
,且前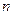 项和
项和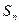 满足
满足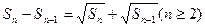
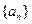 和
和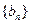 的通项公式;
的通项公式;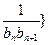 前
前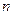 项和为
项和为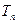 ,问
,问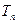 >
>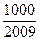 的最小正整数
的最小正整数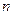 是多少? .
是多少? . 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com