Question

【题目】【2018河南安阳市高三一模】如下图，在平面直角坐标系中，直线与直线之间的阴影部分即为，区域中动点到的距离之积为1．

（Ⅰ）求点的轨迹的方程；

（Ⅱ）动直线穿过区域，分别交直线于两点，若直线与轨迹有且只有一个公共点，求证： 的面积恒为定值．

Answer 1

【答案】（Ⅰ）；（Ⅱ）见解析．

【解析】试题分析：

（Ⅰ）由点到直线距离公式直接把已知表示出来，并化简可得方程；

（Ⅱ）直线与轨迹有且只有一个公共点，即直线与轨迹相切，因此可求出当与垂直（即斜率不存在）时， 面积，当斜率存在时，可设其方程为，与双曲线方程联立方程组，由可得，再设出，由直线相交可求得（用表示），计算面积可得结论.

试题解析：

（Ⅰ）由题意得， .

因为点在区域内，所以与同号，得，

即点的轨迹的方程为.

（Ⅱ）设直线与轴相交于点，当直线的斜率不存在时， ， ，得.

当直线的斜率存在时，设其方程为，显然，则，

把直线的方程与联立得，

由直线与轨迹有且只有一个公共点，知，

得，得或.

设， ，由得，同理，得.

所以 .

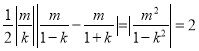综上， 的面积恒为定值2.