
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:不详 题型:解答题
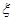 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
一次购物量 (件) (件) | 1≤n≤3 | 4≤n≤6 | 7≤n≤9 | 10≤n≤12 | n≥13 |
| 顾客数(人) |  | 20 | 10 | 5 |  |
| 结算时间(分钟/人) | 0.5 | 1 | 1.5 | 2 | 2.5 |
 与
与 的值;
的值; 的分布列与数学期望;
的分布列与数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,获得50元奖金的概率为
,获得50元奖金的概率为 .
. 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,记
,记 .
. 的分布列及数学期望;
的分布列及数学期望; 在区间(2,3)上有且只有一个零点”为事件
在区间(2,3)上有且只有一个零点”为事件 ,求事件
,求事件  发生的概率.
发生的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com