
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF 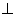 平面EFDC.
平面EFDC.
(Ⅰ) 当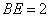 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点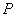 ,且
,且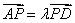 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出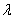 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ) 设BE=x,问当x为何值时,三棱锥A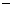 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
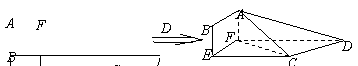 |
【解析】
(Ⅰ)假设存在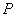 使得满足条件CP∥平面ABEF
使得满足条件CP∥平面ABEF
在平面EFDC内过点C作CM∥EF交DF于M,在平面ADF内作直线MP∥AF交AD于点P,连PC
∵CM∥EF,EF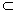 平面ABEF,CM
平面ABEF,CM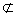 平面ABEF
平面ABEF
∴CM∥平面ABEF
∵PM∥AF,AF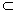 平面ABEF,PM
平面ABEF,PM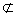 平面ABEF
平面ABEF
∴PM∥平面ABEF
又∵CM PM=M
PM=M
∴平面ABEF∥平面PCM
又∵PC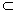 平面PCM
平面PCM
∴PC∥平面ABEF,故点P就是所求的点
又∵FM=4,MD=2
∴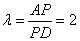
(Ⅱ)因为平面ABEF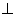 平面EFDC,平面ABEF
平面EFDC,平面ABEF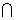 平面EFDC=EF,又AF
平面EFDC=EF,又AF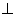 EF,
EF,
所以AF⊥平面EFDC
由已知BE=x,所以AF=x (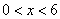 ),则FD=8
),则FD=8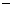 x.
x.
∴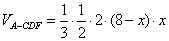
故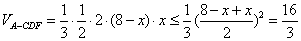
当且仅当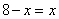 ,即x=4时,等号成立
,即x=4时,等号成立
所以,当x=4时,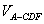 有最大值,最大值为
有最大值,最大值为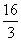
解法二:
故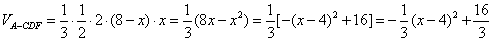
所以,当x=4时,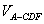 有最大值,最大值为
有最大值,最大值为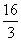


科目:高中数学 来源: 题型:
设a=(sin 17°+cos 17°),b=2cos213°-1,c=,则a,b,c的大小关系( )
A.c<a<b B.a<c<b C.b<a<c D.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
以下说法,正确的个数为:( )
①公安人员由罪犯的脚印的尺寸 估计罪犯的身高情况,所运用的是类比推理.
估计罪犯的身高情况,所运用的是类比推理.
②农谚“瑞雪兆丰年”是通过归纳推理得到的.
③由平面几何中圆的一些性质,推测出球的某些性质这是运用的类比推理.
④个位是5的整数是5的倍数,2375的个位是5,因此2375是5的倍数,这是运用的演绎推理.
A.0 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com