
证明下列命题:
(1)若函数f(x)可导且为周期函数,则f'(x)也为周期函数;
(2)可导的奇函数的导函数是偶函数.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和两平面的交线平行.
请对上面定理加以证明,并说出定理的名称及作用.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于任意两个正整数 ,定义某种运算“※”,法则如下:当
,定义某种运算“※”,法则如下:当 都是正奇数时,
都是正奇数时,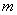 ※
※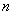 =
=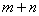 ;当
;当 不全为正奇数时,
不全为正奇数时,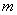 ※
※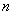 =
=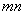 。则在此定义下,集合
。则在此定义下,集合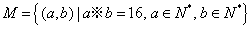 中的元素个数是
中的元素个数是
A. 7 B. 11 C. 13 D. 14
查看答案和解析>>
科目:高中数学 来源: 题型:
某国庆纪念品,每件成本为30元,每卖出一件产品需向税务部门上缴a元(a为常数,4≤a≤6)的税收.设每件产品的售价为x元,根据市场调查,当35≤x≤40时日销售量与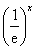 (e为自然对数的底数)成正比.当40≤x≤50时日销售量与
(e为自然对数的底数)成正比.当40≤x≤50时日销售量与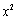 成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
(1)求L(x)关于x的函数关系式;
(2)当每件产品的售价x为多少元时,才能使L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
若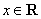 ,用
,用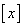 表示不超过
表示不超过 的最大整数(如
的最大整数(如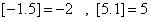 ).设
).设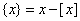 ,则对函数
,则对函数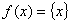 ,下列说法中正确的个数是( )
,下列说法中正确的个数是( )
①定义域为R,值域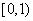
②它是以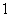 为周期的周期函数
为周期的周期函数
③若方程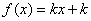 有三个不同的根,则实数
有三个不同的根,则实数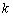 的取值范围是
的取值范围是
④若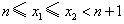
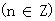 ,则
,则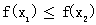
A. 1 B.2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知极点为直角坐标系的原点,极轴为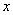 轴正半轴且单位长度相同的极坐标系中,
轴正半轴且单位长度相同的极坐标系中,
直线 :
: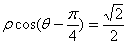 与直角坐标系中的曲线C:
与直角坐标系中的曲线C: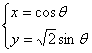 (
(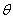 为参数),
为参数),
交于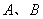 两点.
两点.
(Ⅰ)求直线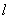 在直角坐标系下的方程;(Ⅱ)求点
在直角坐标系下的方程;(Ⅱ)求点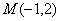 与
与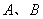 两点的距离之积
两点的距离之积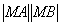 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com