
【题目】已知:已知函数f(x)=﹣ ![]() +2ax,
+2ax,
(Ⅰ)若曲线y=f(x)在点P(2,f(2))处的切线的斜率为﹣6,求实数a;
(Ⅱ)若a=1,求f(x)的极值;
(Ⅲ)当0<a<2时,f(x)在[1,4]上的最小值为﹣ ![]() ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
【答案】解:(Ⅰ)因为f′(x)=﹣x2+x+2a,
曲线y=f(x)在点P(2,f(2))处的切线的斜率k=f′(2)=2a﹣2,
2a﹣2=﹣6,a=﹣2
(Ⅱ)当a=1时, ![]() ,f′(x)=﹣x2+x+2=﹣(x+1)(x﹣2)
,f′(x)=﹣x2+x+2=﹣(x+1)(x﹣2)
x | (﹣∞,﹣1) | ﹣1 | (﹣1,2) | 2 | (2,+∞) |
f′(x) | ﹣ | 0 | + | 0 | ﹣ |
f(x) | 单调减 |
| 单调增 |
| 单调减 |
所以,f(x)的极大值为 ![]() ,f(x)的极小值为
,f(x)的极小值为 ![]() .
.
(Ⅲ)令f′(x)=0,得 ![]() ,
, ![]() ,
,
f(x)在(﹣∞,x1),(x2,+∞)上单调递减,在(x1,x2)上单调递增,
当0<a<2时,有x1<1<x2<4,所以f(x)在[1,4]上的最大值为f(x2),f(4)<f(1),
所以f(x)在[1,4]上的最小值为 ![]() ,解得:a=1,x2=2.
,解得:a=1,x2=2.
故f(x)在[1,4]上的最大值为 ![]()
【解析】1、求出曲线y=f(x)在点P(2,f(2))处的导数值等于切线的斜率-6,即可求出实数a的值。
2、通过a=1利用导函数为0,判断导数符号即可求得f(x)的极值。
3、根据题意可得当0<a<2时利用导函数的单调性通过f(x)在[1,4]上的最小值为-![]() 即可求a进而可得f(x)在[1,4]上的最大值。
即可求a进而可得f(x)在[1,4]上的最大值。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】观察下列各式: C ![]() =40;
=40;
C ![]() +C
+C ![]() =41;
=41;
C ![]() +C
+C ![]() +C
+C ![]() =42;
=42;
C ![]() +C
+C ![]() +C
+C ![]() +C
+C ![]() =43;
=43;
…
照此规律,当n∈N*时,
C ![]() +C
+C ![]() +C
+C ![]() +…+C
+…+C ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知n∈N* , Sn=(n+1)(n+2)…(n+n), ![]() .
.
(Ⅰ)求 S1 , S2 , S3 , T1 , T2 , T3;
(Ⅱ)猜想Sn与Tn的关系,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a2=1,|an+1﹣an|= ![]() ,若a2n+1>a2n﹣1 , a2n+2<a2n(n∈N+)则数列{(﹣1)nan}的前40项的和为( )
,若a2n+1>a2n﹣1 , a2n+2<a2n(n∈N+)则数列{(﹣1)nan}的前40项的和为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面ABCD,AB∥CD,CD⊥AC,过CD的平面分别与PA,PB交于点E,F.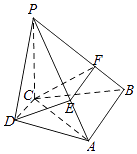
(1)求证:CD⊥平面PAC;
(2)求证:AB∥EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com