
(本小题满分16分)
已知函数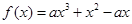 ,其中
,其中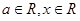 .
.
(1)当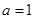 时,求函数
时,求函数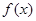 在
在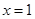 处的切线方程;
处的切线方程;
(2)若函数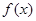 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求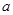 的取值范围;
的取值范围;
(3)已知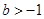 ,如果存在
,如果存在 ,使得函数
,使得函数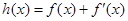
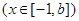 在
在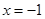 处取得最小值,试求
处取得最小值,试求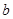 的最大值.
的最大值.
(1)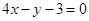 (2)
(2) (3)
(3)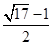
解析试题分析:(1)当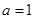 时,
时,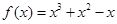 ,则
,则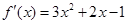 ,故
,故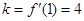 ………2分
………2分
又切点为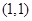 ,故所求切线方程为
,故所求切线方程为 ,即
,即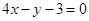 ……………………4分
……………………4分
(2)由题意知,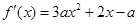 在区间(1,2)上有不重复的零点,
在区间(1,2)上有不重复的零点,
由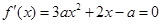 ,得
,得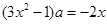 ,因为
,因为 ,所以
,所以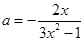 ……7分
……7分
令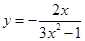 ,则
,则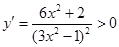 ,故
,故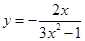 在区间(1,2)上是增函数,
在区间(1,2)上是增函数,
所以其值域为 ,从而
,从而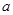 的取值范围是
的取值范围是 ……………………………9分
……………………………9分
(3)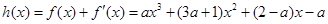 ,
,
由题意知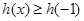 对
对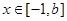 恒成立,即
恒成立,即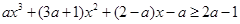 对
对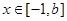 恒成立,即
恒成立,即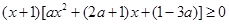 ①对
①对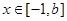 恒成立 ……………………………11分
恒成立 ……………………………11分
当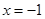 时,①式显然成立;
时,①式显然成立;
当 时,①式可化为
时,①式可化为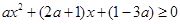 ②,
②,
令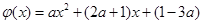 ,则其图象是开口向下的抛物线,所以
,则其图象是开口向下的抛物线,所以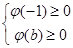 ……………13分
……………13分
即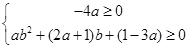 ,其等价于
,其等价于 ③ ,
③ ,
因为③在 时有解,所以
时有解,所以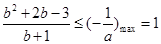 ,解得
,解得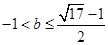 ,
,
从而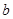 的最大值为
的最大值为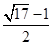 ……………………………16分
……………………………16分
考点:导数的几何意义及函数零点,不等式与函数的转化
点评:不等式恒成立问题常转化为函数最值问题,不等式问题常转化为函数问题求解


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设 ,点P(
,点P( ,0)是函数
,0)是函数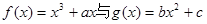 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(1)用 表示a,b,c;
表示a,b,c;
(2)若函数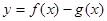 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
已知函数f(x)=lnx+
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2 l+ 1n22,+…+ln2 n> ∈N*).
∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数 ,
,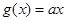 ,
,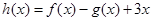 ,其中
,其中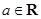 且
且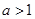 .
.
(I)求函数 的导函数
的导函数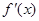 的最小值;
的最小值;
(II)当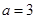 时,求函数
时,求函数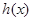 的单调区间及极值;
的单调区间及极值;
(III)若对任意的 ,函数
,函数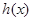 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
设 是定义在
是定义在 上的奇函数,函数
上的奇函数,函数 与
与 的图象关于
的图象关于 轴对称,且当
轴对称,且当 时,
时, .
.
(I)求函数 的解析式;
的解析式;
(II)若对于区间 上任意的
上任意的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com