
【题目】已知四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 在棱
在棱![]() 上且
上且![]() .
.

(1)求证:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)答案见解析(2)![]() (3)
(3)![]()
【解析】
(1)推导出![]() ,从而
,从而![]()
![]() 平面
平面![]() ,进而
,进而![]() ,由此能证明
,由此能证明![]()
![]() 平面
平面![]() ,即可求得答案;
,即可求得答案;
(2)由(1)可得:![]() 平面
平面![]() ,所以
,所以![]() 为
为![]() 与平面
与平面![]() 所成角,求出
所成角,求出![]() 长,即可求得答案;
长,即可求得答案;
(3)连结![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,从而平面
,从而平面![]()
![]() 平面
平面![]() ,进而
,进而![]()
![]() 平面
平面![]() ,过
,过![]() 作
作![]()
![]()
![]() 于点
于点![]() ,连结
,连结![]() ,则
,则![]()
![]()
![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,即可求得答案.
的平面角,即可求得答案.
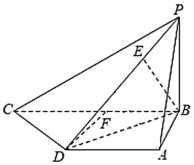
(1)取![]() 中点为
中点为![]() ,连接
,连接![]()
![]()
![]() ,
,
![]()
![]()
![]() 底面
底面![]() 是直角梯形,
是直角梯形,
![]()
![]() ∥
∥![]() ,即
,即![]() ∥
∥![]()
又![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
可得![]() ,
,![]() 中点为
中点为![]() ,
,
根据直角三角形性质可得:![]() 为直角三角形,且
为直角三角形,且![]()
![]()
![]()
又![]()
![]() 平面
平面![]()
![]()
![]()
![]() 平面
平面![]()
![]()
![]()
![]() 平面
平面![]()
![]()
(2)由(1)可得:![]() 平面
平面![]()
![]()
![]() 为
为![]() 与平面
与平面![]() 所成角
所成角
![]()
![]() 为直角三角形,
为直角三角形,![]() ,
,
又![]()
![]() ,
,![]()
![]()
![]() 为等腰直角三角形
为等腰直角三角形
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.
(3)连结![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,如图:
,如图:

![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
![]()
![]()
![]() 平面
平面![]()
过![]() 作
作![]()
![]()
![]() 于点
于点![]() ,连结
,连结![]() ,则
,则![]()
![]()
![]() ,
,
![]()
![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,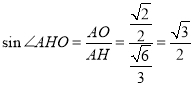
![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中“sinA>sinB”是“cosA<cosB”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是水资源匮乏国家,节约用水是每个中国公民应有的意识.为了保护水资源,提倡节约用水,某城市对居民生活用水实行“阶梯水价”,计费方法如下表:
每户每月用水量 | 水价 |
不超过12 | 3元/ |
超过12 | 6元/ |
超过18 | 9元/ |
(1)该城市居民小张家月用水量记为![]() ,应交纳水费y(元),试建立y与x的函数解析式,并作出其图像;
,应交纳水费y(元),试建立y与x的函数解析式,并作出其图像;
(2)若小张家十月份交纳水费90元,求他家十月份的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上恰有一个实数解,求
上恰有一个实数解,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() 使得函数
使得函数![]() 在区间
在区间![]() 上的最大值和最小值的差不超过1,求
上的最大值和最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有1200名学生,随机抽出300名进行调查研究,调查者设计了一个随机化装置,这是一个装有大小、形状和质量完全相同的10个红球,10个绿球和10个白球的袋子.调查中有两个问题:
问题1:你的阳历生日月份是不是奇数?
问题2:你是否抽烟?
每个被调查者随机从袋中摸出1个球(摸出后再放回袋中).若摸到红球就如实回答第一个问题,若摸到绿球,则不回答任何问题;若摸到白球,则如实回答第二个问题.所有回答“是”的调查者只需往一个盒子中放一个小石子,回答“否”的被调查者什么也不用做.最后收集回来53个小石子,估计该学校吸烟的人数有多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面ABCD为矩形,点E在线段PA上,
中,底面ABCD为矩形,点E在线段PA上,![]() 平面BDE.
平面BDE.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() 是等边三角形,
是等边三角形,![]() ,平面
,平面![]() 平面ABCD,四棱锥
平面ABCD,四棱锥![]() 的体积为
的体积为![]() ,求点E到平面PCD的距离.
,求点E到平面PCD的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数对
,若存在实数对![]() ,使得等式
,使得等式![]() 对定义域中的任意
对定义域中的任意![]() 都成立,则称函数
都成立,则称函数![]() 是“
是“![]() 型函数”.
型函数”.
(1)若函数![]() 是“
是“![]() 型函数”,且
型函数”,且![]() ,求出满足条件的实数对
,求出满足条件的实数对![]() ;
;
(2)已知函数![]() .函数
.函数![]() 是“
是“![]() 型函数”,对应的实数对
型函数”,对应的实数对![]() 为
为![]() ,当
,当![]() 时,
时,![]() .若对任意
.若对任意![]() 时,都存在
时,都存在![]() ,使得
,使得![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com