练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图1­2，在△ABC中，∠B＝，AB＝8，点D在BC边上，且CD＝2，cos∠ADC＝.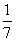

    (1)求sin∠BAD；

    (2)求BD，AC的长．

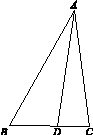
    图1­2


    解：(1) 在△ADC中，因为cos ∠ADC＝，所以sin ∠ADC＝.

    所以sin ∠BAD＝sin(∠ADC－∠B)＝sin ∠ADCcos B－cos ∠ADCsin B＝×－×＝.

    (2)在△ABD中，由正弦定理得

    BD＝＝

    在△ABC中，由余弦定理得

    AC2＝AB2＋BC2－2AB·BC·cos B

    ＝82＋52－2×8×5×＝49，

    所以AC＝7.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     已知条件；条件，若是的充分不必要条件，则实数的取值范围是（  ）

    A.             B.            C.     D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某实验室一天的温度(单位：℃)随时间t(单位：h)的变化近似满足函数关系：

    f(t)＝10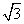－cos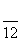t－sin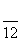t，t∈[0，24)．

    (1)求实验室这一天的最大温差．

    (2)若要求实验室温度不高于11℃，则在哪段时间实验室需要降温？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝sin

    (1)求f(x)的单调递增区间；

    (2)若α是第二象限角，cos 2α，求cos α－sin α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某实验室一天的温度(单位：℃)随时间t(单位：h)的变化近似满足函数关系：

    (1)求实验室这一天的最大温差．

    (2)若要求实验室温度不高于11℃，则在哪段时间实验室需要降温？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，c分别为△ABC三个内角A，B，C的对边，a＝2，且(2＋b)·(sin A－sin B)＝(c－b)sin C，则△ABC面积的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某实验室一天的温度(单位：℃)随时间t(单位：h)的变化近似满足函数关系：

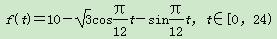    (1)求实验室这一天的最大温差．

    (2)若要求实验室温度不高于11℃，则在哪段时间实验室需要降温？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数．

    (1)当 时，求的最值；

    (2)求实数的取值范围，使在区间上是单调函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    解关于的不等式 ()

    查看答案和解析>>

    同步练习册答案