
【题目】(1)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值
的最大值![]() ;
;
(2)在(1)的条件下,求证:函数![]() 在区间
在区间![]() 内存在唯一的极大值点
内存在唯一的极大值点![]() ,且
,且![]() .
.
【答案】(1)![]() .(2)家粘结性
.(2)家粘结性
【解析】
(1)令![]() ,求出导函数
,求出导函数![]() ,由
,由![]() 确定增区间,
确定增区间,![]() 确定减区间,从而得
确定减区间,从而得![]() 的最小值,得
的最小值,得![]() 的取值范围,即得
的取值范围,即得![]() ;
;
(2)求出导函数![]() ,通分后,令
,通分后,令![]() ,再求导数
,再求导数![]() ,令
,令![]() .分类讨论,当
.分类讨论,当![]() 时,
时,![]() ,得
,得![]() 递减,从而可得
递减,从而可得![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,
,![]() 时,令
时,令![]() .利用导数得
.利用导数得![]() 的单调性,从而得
的单调性,从而得![]() ,于是得出在
,于是得出在![]() 上
上![]() 的单调性,得唯一极大值点
的单调性,得唯一极大值点![]() .由
.由![]() 可对
可对![]() 变形,得
变形,得![]() ,只要证明在
,只要证明在![]() 上
上![]() ,从而可证得结论.
,从而可证得结论.
(1)解:令![]() ,则
,则![]() .
.
可见,![]() ;
;![]() .
.
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以,当且仅当![]() 时,函数
时,函数![]() 取最小值1.
取最小值1.
由题意,实数![]() .所以
.所以![]() .
.
(2)由(1),![]() .
.
令![]() ,
,
则![]() .
.
令![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
可见,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
又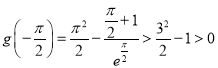 (由(1),可得
(由(1),可得![]() ,所以
,所以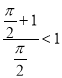 ),
),
![]() ,所以存在唯一的
,所以存在唯一的![]() ,使得
,使得![]() .
.
从而,当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减.
单调递减.
②当![]() 时,令
时,令![]() .
.
则![]() .所以
.所以![]() 在
在![]() 上单调递减.
上单调递减.
所以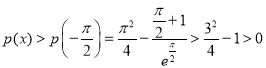 (由(1),可得
(由(1),可得![]() ,所以
,所以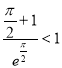 ).
).
又当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,从而
,从而![]() .所以
.所以![]() 在
在![]() 单调递增.
单调递增.
综上所述,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单词递减.
上单词递减.
所以,函数![]() 在区间
在区间![]() 内存在唯一极大值点
内存在唯一极大值点![]() .
.
关于![]() 的证明如下:
的证明如下:
由上面的讨论,![]() ,且
,且![]() ,所以
,所以![]() ,所以
,所以![]() .
.
于是![]() .
.
令![]() .当
.当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 上单调递增.所以,当
上单调递增.所以,当![]() 时,
时,![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() .
.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
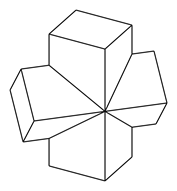
【题目】如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体有________个面,其体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.由于盒子上没有标注,购买者只有打开才会知道自己买到了什么,因此这种惊喜吸引了众多年轻人,形成了“盲盒经济”.某款盲盒内可能装有某一套玩偶的![]() 、
、![]() 、
、![]() 三种样式,且每个盲盒只装一个.
三种样式,且每个盲盒只装一个.
(1)若每个盲盒装有![]() 、
、![]() 、
、![]() 三种样式玩偶的概率相同.某同学已经有了
三种样式玩偶的概率相同.某同学已经有了![]() 样式的玩偶,若他再购买两个这款盲盒,恰好能收集齐这三种样式的概率是多少?
样式的玩偶,若他再购买两个这款盲盒,恰好能收集齐这三种样式的概率是多少?
(2)某销售网点为调查该款盲盒的受欢迎程度,随机发放了200份问卷,并全部收回.经统计,有![]() 的人购买了该款盲盒,在这些购买者当中,女生占
的人购买了该款盲盒,在这些购买者当中,女生占![]() ;而在未购买者当中,男生女生各占
;而在未购买者当中,男生女生各占![]() .请根据以上信息填写下表,并分析是否有
.请根据以上信息填写下表,并分析是否有![]() 的把握认为购买该款盲盒与性别有关?
的把握认为购买该款盲盒与性别有关?
女生 | 男生 | 总计 | |
购买 | |||
未购买 | |||
总计 |
参考公式: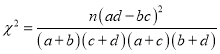 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)该销售网点已经售卖该款盲盒6周,并记录了销售情况,如下表:
周数 | 1 | 2 | 3 | 4 | 5 | 6 |
盒数 | 16 | ______ | 23 | 25 | 26 | 30 |
由于电脑故障,第二周数据现已丢失,该销售网点负责人决定用第4、5、6周的数据求线性回归方程,再用第1、3周数据进行检验.
①请用4、5、6周的数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(注: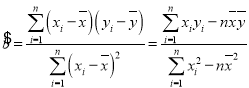 ,
,![]() )
)
②若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2盒,则认为得到的线性回归方程是可靠的,试问①中所得的线性回归方程是否可靠?
③如果通过②的检验得到的回归直线方程可靠,我们可以认为第2周卖出的盒数误差也不超过2盒,请你求出第2周卖出的盒数的可能取值;如果不可靠,请你设计一个估计第2周卖出的盒数的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为1.
截得的弦长为1.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 两点,与线段
两点,与线段![]() 和椭圆短轴分别交于两个不同点
和椭圆短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对一切正整数
,且对一切正整数![]() 都有
都有![]() .
.
(1)求证:![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在实数![]() ,使不等式
,使不等式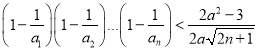 ,对一切正整数
,对一切正整数![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
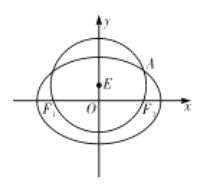
【题目】如图,已知圆![]() 经过椭圆
经过椭圆![]() 的左右焦点
的左右焦点![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
(1)求椭圆![]() 的方程;
的方程;
(2)设与直线![]() (
(![]() 为原点)平行的直线交椭圆
为原点)平行的直线交椭圆![]() 于
于![]() 两点,当
两点,当![]() 的面积取取最大值时,求直线
的面积取取最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用字母![]() 表示.我们可以通过设计一个试验来估计
表示.我们可以通过设计一个试验来估计![]() 的值:从
的值:从![]() 表示的区域内随机抽取200个实数对
表示的区域内随机抽取200个实数对![]() ,其中x,y两个数能与1构成钝角三角形三边长的数对
,其中x,y两个数能与1构成钝角三角形三边长的数对![]() 共有56个.则用随机模拟的方法估计
共有56个.则用随机模拟的方法估计![]() 的近似值为________.
的近似值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com