
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对一切正整数
,且对一切正整数![]() 都有
都有![]() .
.
(1)求证:![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在实数![]() ,使不等式
,使不等式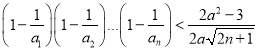 ,对一切正整数
,对一切正整数![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在;
;(3)存在;![]() 的取值范围是
的取值范围是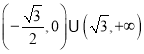 .
.
【解析】
(1)由题得![]() ①,
①,![]() ②,②-①即得
②,②-①即得![]() ;
;
(2)由题得![]() .
.![]() ,再对
,再对![]() 分奇数和偶数两种情况讨论,求出数列
分奇数和偶数两种情况讨论,求出数列![]() 的通项公式;
的通项公式;
(3)令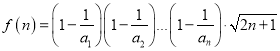
![]() ,判断函数的单调性,求出其最大值,解不等式
,判断函数的单调性,求出其最大值,解不等式![]() 即得解.
即得解.
(1)证明:∵![]() ①,
①,
∴![]() ②
②
由②-①得![]() ,
,
∴![]() .
.
(2)∵![]() ③
③
∴![]() ,④
,④
④-③,得![]() .
.![]()
从而数列![]() 的奇数项依次成等差数列,且首项为
的奇数项依次成等差数列,且首项为![]() ,公差为
,公差为![]() ;
;
数列![]() 的偶数项也依次成等差数列,且首项为
的偶数项也依次成等差数列,且首项为![]() ,公差为
,公差为![]() .
.
在①中令![]() 得
得![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
在③中令![]() 得
得![]() ,∴
,∴![]() .
.
∴当![]() 时,
时,![]() ,
,![]() ;
;
∴当![]()
![]() 时,
时,![]() ,
,![]() ;
;
综上所述,![]() .
.
(3)令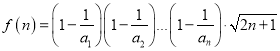
![]() ,则
,则![]()
且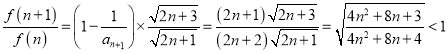
∴![]() ,
,
∴![]() 单调递减,
单调递减,
∴![]() .
.
∴不等式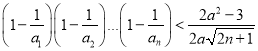 对一切正整数
对一切正整数![]() 都成立等价于
都成立等价于![]() 对一切正整数
对一切正整数![]() 都成立,
都成立,
等价于![]() ,即
,即![]() .
.
∴![]() ,即
,即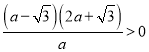 ,
,
解之得![]() ,或
,或![]() .
.
综上所述,存在实数![]() 的适合题意,
的适合题意,![]() 的取值范围是
的取值范围是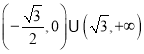 .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】2019年女排世界杯(第13届女排世界杯)是由国际排联![]() 举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球
举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球![]() _
_![]() ,已知这种球的质量指标ξ(单位:
,已知这种球的质量指标ξ(单位:![]() )服从正态分布
)服从正态分布![]() .比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以
.比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以![]() 或
或![]() 取胜的球队积3分,负队积0分;而在比赛中以
取胜的球队积3分,负队积0分;而在比赛中以![]() 取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为
取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)如果比赛准备了1000个排球,估计质量指标在![]() 内的排球个数(计算结果取整数)
内的排球个数(计算结果取整数)
(2)第10轮比赛中,记中国队![]() 取胜的概率为
取胜的概率为![]() ,求出
,求出![]() 的最大值点
的最大值点![]() ,并以
,并以![]() 作为p的值,解决下列问题.
作为p的值,解决下列问题.
(i)在第10轮比赛中,中国队所得积分为X,求X的分布列;
(ii)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
参考数据:![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,g(x)= ![]() (a∈R,e为自然对数的底数)
(a∈R,e为自然对数的底数)
(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在![]() 上无零点,求a的最小值;
上无零点,求a的最小值;
(Ⅲ)若对任意给定的x0∈(0,e],在(0,e]上总存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
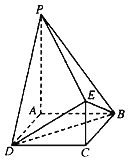
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数是简化繁杂运算的产物.16世纪时,为了简化数值计算,数学家希望将乘除法归结为简单的加减法.当时已经有数学家发现这在某些情况下是可以实现的.
比如,利用以下2的次幂的对应表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16与256;然后找出它们在第一行对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4096,这就是![]() 的值.
的值.
用类似的方法可以算出![]() 的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是
的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是坐标原点,椭圆
是坐标原点,椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆上,若
在椭圆上,若![]() 的面积最大时
的面积最大时![]() 且最大面积为
且最大面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
:![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,点
,点![]() 是第四象限内的点且在椭圆
是第四象限内的点且在椭圆![]() 上,线段
上,线段![]() 被直线
被直线![]() 垂直平分,直线
垂直平分,直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: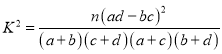 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com