
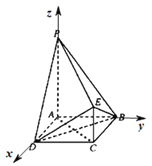
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
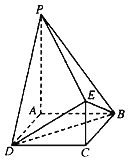
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)连结AC,推导出BD⊥AC,PA⊥BD,PA⊥AD,从而BD⊥平面APEC,进而BD⊥PE,推导出PE⊥DE,由此能证明PE⊥平面DBE.
(2)以A为原点,AD,AB,AP所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣PD﹣E的正弦值.
(1)证明:连结AC,∵四边形ABCD是正方形,
∴BD⊥AC,∵PA⊥平面ABCD,∴PA⊥BD,PA⊥AD,
∵PA∩AC=A,∴BD⊥平面APEC,∵PE平面APEC,
∴BD⊥PE,设AB=1,则AD=1,PA=2,∴PD![]() ,
,
同理解得DE![]() ,在梯形PACE中,解得PE
,在梯形PACE中,解得PE![]() ,
,
∴PE2+DE2=PD2,∴PE⊥DE,∵BD∩DE=D,
∴PE⊥平面DBE.
(2)以A为原点,AD,AB,AP所在直线为x,y,z轴,建立空间直角坐标系,
令AB=1,则CE=1,AP=2,
∴P(0,0,2),E(1,1,1),D(1,0,0),B(0,1,0),
![]() (﹣1,﹣1,1),
(﹣1,﹣1,1),![]() (﹣1,0,2),
(﹣1,0,2),![]() (0,﹣1,2),
(0,﹣1,2),
![]() (1,﹣1,0),设平面DPE的法向量
(1,﹣1,0),设平面DPE的法向量![]() (x,y,z),
(x,y,z),
则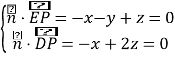 ,取z=1,得
,取z=1,得![]() (2,﹣1,1),
(2,﹣1,1),
设平面BPD的法向量![]() (a,b,c),
(a,b,c),
则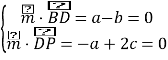 ,取c=1,得
,取c=1,得![]() (2,2,1),
(2,2,1),
则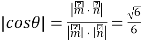 ,
,
∴二面角B﹣PD﹣E的正弦值sinθ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】受新冠肺炎疫情影响,某学校按上级文件指示,要求错峰放学,错峰有序吃饭.高三年级一层楼六个班排队,甲班必须排在前三位,且丙班、丁班必须排在一起,则这六个班排队吃饭的不同安排方案共有( )
A.240种B.120种C.188种D.156种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)不需证明,直接写出![]() 的奇偶性:
的奇偶性:
(Ⅱ)讨论![]() 的单调性,并证明
的单调性,并证明![]() 有且仅有两个零点:
有且仅有两个零点:
(Ⅲ)设![]() 是
是![]() 的一个零点,证明曲线
的一个零点,证明曲线![]() 在点
在点![]() 处的切线也是曲线
处的切线也是曲线![]() 的切线.
的切线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对一切正整数
,且对一切正整数![]() 都有
都有![]() .
.
(1)求证:![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在实数![]() ,使不等式
,使不等式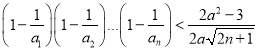 ,对一切正整数
,对一切正整数![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和圆
和圆![]() ,
,![]() 、
、![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(I)求![]() 的方程;
的方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com