
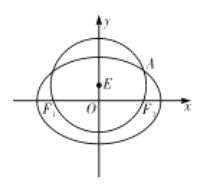
【题目】如图,已知圆![]() 经过椭圆
经过椭圆![]() 的左右焦点
的左右焦点![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
(1)求椭圆![]() 的方程;
的方程;
(2)设与直线![]() (
(![]() 为原点)平行的直线交椭圆
为原点)平行的直线交椭圆![]() 于
于![]() 两点,当
两点,当![]() 的面积取取最大值时,求直线
的面积取取最大值时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由题意把焦点坐标代入圆的方程求出![]() ,再由条件得
,再由条件得![]() 为圆
为圆![]() 的直径,且
的直径,且![]() ,根据勾股定理求出
,根据勾股定理求出![]() ,根据椭圆的定义和
,根据椭圆的定义和![]() 依次求出
依次求出![]() 的值,代入椭圆方程即可;
的值,代入椭圆方程即可;
(2)由(1)求出![]() 的坐标,根据向量共线的条件求出直线
的坐标,根据向量共线的条件求出直线![]() 的斜率,设直线
的斜率,设直线![]() 的方程和
的方程和![]() 的坐标,联立直线方程和椭圆方程消去
的坐标,联立直线方程和椭圆方程消去![]() ,利用韦达定理和弦长公式求出
,利用韦达定理和弦长公式求出![]() ,由点到直线的距离公式求出点
,由点到直线的距离公式求出点![]() 到直线
到直线![]() 的距离,代入三角形的面积公式求出
的距离,代入三角形的面积公式求出![]() ,化简后求最值即可.
,化简后求最值即可.
试题解析:(1)∵![]() ,
, ![]() ,
, ![]() 三点共线,∴
三点共线,∴![]() 为圆
为圆![]() 的直径,且
的直径,且![]() ,
,
∴![]() .由
.由![]() ,得
,得![]() ,∴
,∴![]() ,∵
,∵![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() . (2)由(1)知,点
. (2)由(1)知,点![]() 的坐标为
的坐标为![]() ,∴直线
,∴直线![]() 的斜率为
的斜率为![]() ,故设直线
,故设直线![]() 的方程为
的方程为![]() ,将
,将![]() 方程代入
方程代入![]() 消去
消去![]() 得:
得: ![]() , 设
, 设![]()
![]() ∴
∴![]() ,
, ![]() ,
, ![]() ,
,![]() ∴
∴![]() , 又:
, 又:
![]() =
=![]() ,∵点
,∵点![]() 到直线
到直线![]() 的距离
的距离![]() , ∴
, ∴![]()
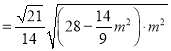
![]()
![]() ,
,
当且仅当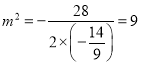 ,即
,即![]() 时等号成立,此时直线
时等号成立,此时直线![]() 的方程为
的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】为响应国家扩大内需的政策,某厂家拟在2016年举行某一产品的促销获得,经调查测算,该产品的年销量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元满足
万元满足![]() (
(![]() 为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(成产投入成本包括生产固定投入和生产再投入两部分).
为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(成产投入成本包括生产固定投入和生产再投入两部分).
(1)求常数![]() ,并将该厂家2016年该产品的利润
,并将该厂家2016年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2016年的年促销费用投入多少万元时,厂家利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
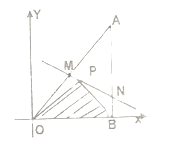
【题目】如图所示,将一块直角三角形木板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角形木板内一点,现因三角形木板中阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角形木板锯成
将三角形木板锯成![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求点![]() 的坐标及直线
的坐标及直线![]() 的斜率
的斜率![]() 的范围;
的范围;
(Ⅱ)令![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的取值范围;
的取值范围;
(Ⅲ)令(Ⅱ)中![]() 的取值范围为集合
的取值范围为集合![]() ,若
,若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为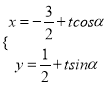 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,( ![]() )
)
(1)写出直线![]() 经过的定点的直角坐标,并求曲线
经过的定点的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)若![]() ,求直线
,求直线![]() 的极坐标方程,以及直线
的极坐标方程,以及直线![]() 与曲线
与曲线![]() 的交点的极坐标.
的交点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1 . 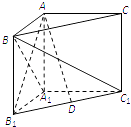
(1)求证:AB1⊥平面A1BC1;
(2)若D为B1C1的中点,求AD与平面A1BC1所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com