
已知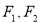 是椭圆
是椭圆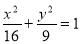 的两个焦点,过
的两个焦点,过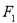 的直线与椭圆交于M、N两点,则
的直线与椭圆交于M、N两点,则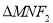 的周长为
的周长为
A. 16 B. 8 C. 25 D. 32
科目:高中数学 来源:2015届福建省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
下列命题的说法错误的是( ).
A.命题“若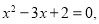 则
则 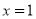 ”的逆否命题为:“若
”的逆否命题为:“若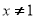 , 则
, 则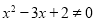 ”.
”.
B.“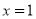 ”是“
”是“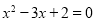 ”的充分不必要条件.
”的充分不必要条件.
C.对于命题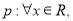
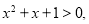 则
则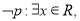
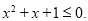
D.若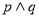 为假命题,则
为假命题,则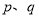 均为假命题.
均为假命题.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期中考理科数学试卷(解析版) 题型:选择题
如果对定义在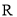 上的函数
上的函数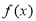 ,对任意两个不相等的实数
,对任意两个不相等的实数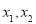 ,都有
,都有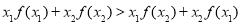 ,则称函数
,则称函数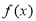 为“
为“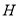 函数”.给出下列函数
函数”.给出下列函数
①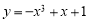 ;②
;②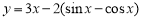 ;③
;③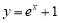 ;④
;④ .以上函数是“
.以上函数是“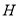 函数”的共有( )
函数”的共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
已知椭圆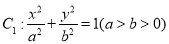 过点
过点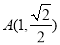 ,其焦距为
,其焦距为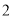 .
.
(Ⅰ)求椭圆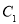 的方程;
的方程;
(Ⅱ)已知椭圆具有如下性质:若椭圆的方程为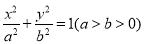 ,则椭圆在其上一点
,则椭圆在其上一点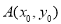 处
处
的切线方程为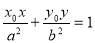 ,试运用该性质解决以下问题:
,试运用该性质解决以下问题:
(i)如图(1),点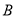 为
为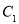 在第一象限中的任意一点,过
在第一象限中的任意一点,过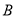 作
作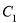 的切线
的切线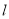 ,
,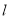 分别与
分别与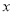 轴和
轴和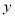 轴的正
轴的正
半轴交于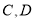 两点,求
两点,求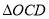 面积的最小值;
面积的最小值;
(ii)如图(2),过椭圆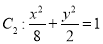 上任意一点
上任意一点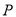 作
作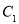 的两条切线
的两条切线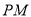 和
和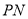 ,切点分别为
,切点分别为
 .当点
.当点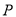 在椭圆
在椭圆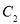 上运动时,是否存在定圆恒与直线
上运动时,是否存在定圆恒与直线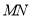 相切?若存在,求出圆的方程;
相切?若存在,求出圆的方程;
若不存在,请说明理由.


查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
椭圆有这样的光学性质:从椭圆的一个焦点发出的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形球盘,点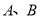 是它的两个焦点,长轴长
是它的两个焦点,长轴长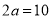 ,焦距
,焦距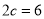 ,静放在点
,静放在点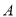 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点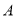 沿直线(不与长轴共线)发出,经椭圆壁反弹后第一次回到点
沿直线(不与长轴共线)发出,经椭圆壁反弹后第一次回到点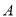 时,小球经过的路程为 .
时,小球经过的路程为 .
查看答案和解析>>
科目:高中数学 来源:2015届福建省晋江市高二下学期期末理科数学试卷(解析版) 题型:解答题
已知矩阵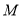 有特征值
有特征值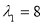 及对应特征向量
及对应特征向量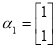 ,且矩阵
,且矩阵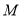 对应的变换将点
对应的变换将点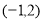 变换成
变换成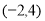
(Ⅰ)求矩阵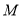 ;
;
(Ⅱ)若直线在矩阵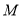 所对应的线性变换作用下得到直线
所对应的线性变换作用下得到直线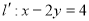 ,求直线方程.
,求直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com