
| A. | 45° | B. | 60° | C. | 90° | D. | 与点P的位置有关 |
分析 如图所示,建立空间直角坐标系.不妨时AB=2,则A(2,0,0),O(1,1,0),M(0,0,1),设P(2,y,2),
计算$\overrightarrow{AM}•\overrightarrow{OP}$,即可得出.
解答 解:如图所示,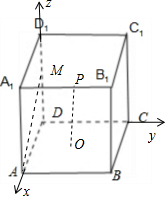 建立空间直角坐标系.
建立空间直角坐标系.
不妨时AB=2,则A(2,0,0),O(1,1,0),M(0,0,1),设P(2,y,2),
则$\overrightarrow{AM}$=(-2,0,1),$\overrightarrow{OP}$=(1,y-1,2),
∴$\overrightarrow{AM}•\overrightarrow{OP}$=-2+0+2=0,
∴$\overrightarrow{AM}⊥\overrightarrow{OP}$.
∴直线OP与直线AM所成的角为90°.
故选:C.
点评 本题考查了数量积运算性质、向量垂直与数量积的关系、异面直线所成的角,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 如图,圆(x+2)2+y2=4的圆心为点B,A(2,0),P是圆上任意一点,线段AP的垂直平分线l和直线BP相交于点Q,当点P在圆上运动时,点Q的轨迹方程为${x^2}-\frac{y^2}{3}=1$.
如图,圆(x+2)2+y2=4的圆心为点B,A(2,0),P是圆上任意一点,线段AP的垂直平分线l和直线BP相交于点Q,当点P在圆上运动时,点Q的轨迹方程为${x^2}-\frac{y^2}{3}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 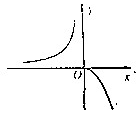 | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
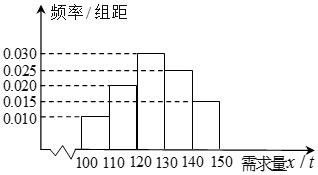 随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 蒜台 | 4吨 | 1.2万元 | 0.55万元 |
| 花菜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | 50万 | B. | 48万 | C. | 47万 | D. | 45万 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com