
高校招生是根据考生所填报的志愿,从考试成绩所达到的最高第一志愿开始,按顺序分批录取,若前一志愿不能录取,则依次给下一个志愿(同批或下一批)录取.某考生填报了三批共6个不同志愿(每批2个),并对各志愿的单独录取以及能考上各批分数线的概率进行预测,结果如“表一”所示(表中的数据为相应的概率,a、b分别为第一、第二志愿).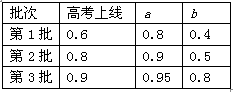
(Ⅰ)求该考生能被第2批b志愿录取的概率;
(Ⅱ)求该考生能被录取的概率;
(Ⅲ)如果已知该考生高考成绩已达到第2批分数线却未能达到第1批分数线,请计算其最有可能在哪个志愿被录取?
(以上结果均保留二个有效数字)
科目:高中数学 来源: 题型:解答题
(本小题满分12分)袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用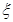 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求:
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量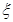 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)计分介于20分到40分之间的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题14分)某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2-6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到.有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.
(1)求x,y,z的值;
(2)求2011年2-6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀.现随机地从上表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附表:我国2010年和2011年2~6月的CPI数据(单位:百分点.注:1个百分点=1%)
| 年份 | 二月 | 三月 | 四月 | 五月 | 六月 |
| 2010 | 2.7 | 2.4 | 2.8 | 3.1 | 2.9 |
| 2011 | 4.9 | 5.0 | x | y | z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某产品按行业生产标准分成 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准 生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取
生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取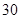 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品.
的为三等品.
(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率;
(2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏中,①摸出3个白球的概率;②获奖的概率;(6分)
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X). (6分)
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
用5,6,7,8,9组成没有重复数字的五位数,其中有且只有一个奇数夹在两个偶数之间的五位数的个数是( )
| A.36 | B.48 | C.72 | D.120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
编号为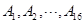 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 | 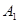 | 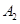 | 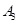 | 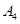 | 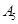 | 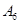 | 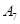 | 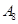 |
| 得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
| 运动员编号 | 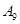 | 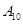 | 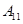 | 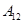 | 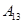 | 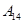 | 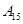 | 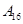 |
| 得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
| 区间 |  | 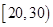 | 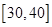 |
| 人数 | | | |
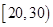 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一种摸奖游戏,一个不透明的袋中装有大小相同的红球5个,白球10个,摸奖者每次随机地从袋中摸出5个球查看后再全部放回,若这5个球中有3个红球则中三等奖,有4个红球则中二等奖,有5个红球则中一等奖.
(1)某人摸奖一次,问他中奖的概率有多大?
(2)某人摸奖一次,若已知他中奖了,问他中二等奖的概率有多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com