练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=lnx+2sinα（α∈（0，））的导函数f′（x），若存在x0＜1使得f′（x0）=f（x0）成立，则实数α的取值范围为（　　）
    A.（ ， ）
    B.（0，）
    C.（ ， ）
    D.（0，）

    【答案】C
    【解析】∵f′（x）= ， f′（x0）= ， f′（x0）=f（x0），
    ∴=ln x0+2sinα，
    ∴sinα=﹣ln x0 ，
    又∵0＜x0＜1，
    ∴可得 （﹣ln x0）＞ ， 即sin α＞ ，
    ∴α∈（ ， ）
    故选：C．
    【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，M、N是焦点为F的抛物线y2=2px（p＞0）上两个不同的点，且线段MN中点A的横坐标为4- ，
    （1）求|MF|+|NF|的值；
    （2）若p=2，直线MN与x轴交于点B点，求点B横坐标的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知AB是半圆O的直径，O是半圆圆心，AB=8，M、N、P是将半圆圆周四等分的三个分点．
    （1）从A、B、M、N、P这5个点中任取3个点，求这3个点组成等腰三角形的概率；
    （2）在半圆内任取一点S，求△SOB的面积大于4 的概率．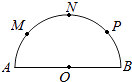

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，长方体ABCD﹣A1B1C1D1中，AA1=AD=1，AB=2，点E是C1D1的中点．
    （1）求证：DE⊥平面BCE；
    （2）求二面角A﹣EB﹣C的大小．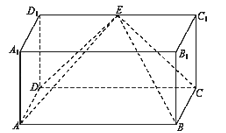

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2 cosB﹣sin（A﹣B）sinB+cos（A+C）=﹣ ．
    （1）求cosA的值；
    （2）若a=4 ，b=5，求向量 在 方向上的投影．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体中， 、分别是、的中点.

    (1)求证：四边形是菱形；

    (2)求异面直线与所成角的大小 (结果用反三角函数值表示) .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，五面体中，四边形是菱形， 是边长为2的正三角形， ， ．

    （1）证明： ；

    （2）若点在平面内的射影，求与平面所成的角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两直线l1：ax﹣by+4=0，l2：（a﹣1）x+y+b=0，求分别满足下列条件的a，b的值．
    （1）直线l1过点（﹣3，﹣1），且l1⊥l2；
    （2）l1∥l2 ， 且坐标原点到l1与l2的距离相等．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是绵阳市某小区100户居民2014年平均用水量（单位：t）的频率分布直方图，则该小区2014年的月平均用水量的众数，中位数的估计值分别是（ ）

    A.2，2.5
    B.2，2.02
    C.2.25，2.5
    D.2.25，2.02

    查看答案和解析>>

    同步练习册答案