【答案】
分析:(Ⅰ)当a=1时,f(x)=-x
3+x
2+x+1,得f(2)=-1,且f′(x)=-3x
2+2x+1,f′(2)=-7.由此能求出曲线y=f(x)在点(2,f(2))处的切线方程.
(Ⅱ)f(x)=-x
3+ax
2+a
2x+1,f′(x)=-3x
2+2ax+a
2=-(3x+a)(x-a),令f(x)=0,解得
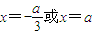
.由于a>0,故
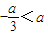
,列表讨论,能够求出函数f(x)的极大值和极小值.
(Ⅲ)若存在满足题意的四边形ABCD,则方程|f(x)-f′(x)|=4至少有两个相异实根,且每个实根对应一条垂直于x轴且与f (x)、f′(x)图象均相交的线段.这些线段长度均相等.由此进行分类讨论,能求出满足题意的平行四边形ABCD有6个.
解答:解:(Ⅰ)当a=1时,f(x)=-x
3+x
2+x+1,得f(2)=-1,
且f′(x)=-3x
2+2x+1,f′(2)=-7.
所以,曲线f(x)在点(2,f(2))处的切线方程是y+1=-7(x-2),
整理得7x+y-13=0.…(3分)
(Ⅱ)f(x)=-x
3+ax
2+a
2x+1,
f′(x)=-3x
2+2ax+a
2=-(3x+a)(x-a)
令f(x)=0,解得
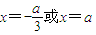
.
由于a>0,故
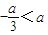
…(4分)
当x变化时,f′(x),f(x)的变化如下表:
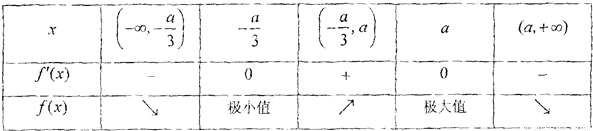
因此,函数
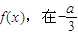
处取得极小值
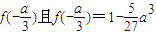
;
函数f(x)在x=a处取得极大值f(a),且f(a)=1+a
3.…(8分)
(Ⅲ)若存在满足题意的四边形ABCD,
则方程|f(x)-f′(x)|=4至少有两个相异实根,
且每个实根对应一条垂直于x轴且与f (x)、f′(x)图象均相交的线段.
这些线段长度均相等.f(x)=-x
3+2x
2+4x+1,
f′(x)=-3x
2+4x+4
=-(3x+2)(x-2)|f(x)-f′(x)|
=|-x
3+2x
2+4x+1-(-3x
2+4x+4)|
=|x
3-5x
2+3|=4…1O分
①当x
3-5x
2+3=4时.x
3-5x-1=0,
令g(x)=x
3-5x
2-1,g′(x)=3x
2-10x
令g′(x)=0,得x=0或
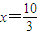
,
当x变化时,g′(x),g(x)的变化如下表:
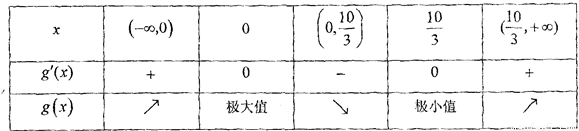
由表格知,g(0)为g(x)的极大值,

为g(x)的极大值,
而
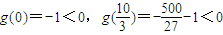
,
故g(x)的图象与x轴有且只有一个交点,g(x)有且只有一个零点. …(11分)
②当x
3-5x
2+3=-4时,x
3-5x
2+7=0,
令g(x)=x
3-5x
2+7,g′(x)=3x
2-10x,
由①知g(0)为g(x)的极大值,
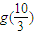
为g(x)的极大值而,
而
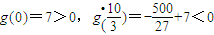
,
故g(x)的图象与x轴有三个交点,g(x)有三个零点,…(12分)
由①②知,方程|x
3-5x
2+3|=4有四个不同的实根,
从小到大依次记为x
1、x
2、x
3、x
4,这四个根对应
的四条线段中的每两条对应一个平行四边形ABCD,
共有(x
1、x
2),(x
1、x
3)
2、x
3),(x
2、x
4),(x
3、x
4)6个,
所以满足题意的平行四边形ABCD有6个.…(14分)
点评:本题考查切线方程的求法,考查函数的最大值和最小值的应用,考查满足条件的四边形的个数的求法.具有一定的探索性,对数学思维的要求较高.解题时要认真审题,仔细解答,注意合理地进行等价转化.

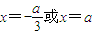 .由于a>0,故
.由于a>0,故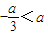 ,列表讨论,能够求出函数f(x)的极大值和极小值.
,列表讨论,能够求出函数f(x)的极大值和极小值.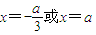 .
.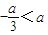 …(4分)
…(4分)
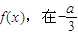 处取得极小值
处取得极小值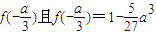 ;
;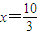 ,
, 由表格知,g(0)为g(x)的极大值,
由表格知,g(0)为g(x)的极大值, 为g(x)的极大值,
为g(x)的极大值,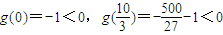 ,
,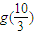 为g(x)的极大值而,
为g(x)的极大值而,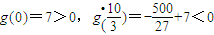 ,
,
