
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() ,
,![]() 底面
底面![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]()

(1)证明:面![]() 面
面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
方法一:(1)由题意,得出![]() ,再由菱形的性质,求得
,再由菱形的性质,求得![]() ,由线面垂直的判定定理,证得
,由线面垂直的判定定理,证得![]() 面
面![]() ,进而利用面面垂直的判定定理,即可得到面
,进而利用面面垂直的判定定理,即可得到面![]() 面
面![]() ;
;
(2)连接OE,证得![]() ,得到
,得到![]() 是二面角
是二面角![]() 的平面角,在
的平面角,在![]() 中,即可求解.
中,即可求解.
法二:(1)以点![]() 为坐标原点,建立如图所示空间直角坐标系,求得平面
为坐标原点,建立如图所示空间直角坐标系,求得平面![]() 的一个法向量为
的一个法向量为![]() ,根据
,根据![]() ,得
,得![]() 面
面![]() ,在面面垂直的判定定理,证得面
,在面面垂直的判定定理,证得面![]() 面
面![]() ;
;
(2)分别求得平面![]() 和平面
和平面![]() 的法向量为
的法向量为![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(1)证明:∵![]() 面
面![]()
∴![]()
∵在菱形![]() 中,
中,![]()
且![]()
∴![]() 面
面![]()
故面![]() 面
面![]()
(2)连接![]() ,则
,则![]() 面
面![]() 面
面![]()
故![]() 在面
在面![]() 内的射影为
内的射影为![]()
∵![]()
∴![]()
![]()
又由(1)可得,![]()
故![]() 是二面角
是二面角![]() 的平面角
的平面角
菱形![]() 中,
中,![]() ,
,![]()
∴![]() ,
,![]()
又![]() 所以
所以![]()
故![]()
∴![]() 即二面角
即二面角![]() 的余弦值为
的余弦值为![]()
法二:(1)菱形![]() 中,
中,![]() 又
又![]() 面
面![]()
故可以以点![]() 为坐标原点,建立如图所示空间直角坐标系
为坐标原点,建立如图所示空间直角坐标系
由![]() 可知相关点坐标如下:
可知相关点坐标如下:
![]()
则平面![]() 的一个法向量为
的一个法向量为![]()
因为![]() 所以
所以![]() 故
故![]() 面
面![]()
从而面![]() 面
面![]()
(2)设![]() ,则
,则![]()
因为![]()
所以![]()
故![]()
可得:![]()
平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 的一个法向量
的一个法向量![]()
则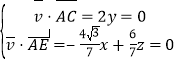 故
故![]()
∴![]()
即二面角![]() 的余弦值为
的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ex+3x2-2x+1+b,x∈R的图象在x=0处的切线方程为y=ax+2.
(1)求函数f(x)的单调区间与极值;
(2)若存在实数x,使得f(x)-2x2-3x-2-2k≤0成立,求整数k的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一研究性学习小组对春季昼夜温差大小与某大豆种子发芽多少之间的关系进行分析研究,他们分别记录了4月1日至4月5日的每天昼夜温差与实验室每天每100颗种子的发芽数,得到如下数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 8 | 12 | 13 | 11 | 10 |
发芽数 | 18 | 26 | 30 | 25 | 20 |
该学习组所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻2天的数据的概率;
(2)若选取的是4月1日与4月5日这2组数据做检验,请根据4月2日至4月4日这3组数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)所得的线性回归方程是否可靠?
参考公式和数据: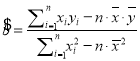 ,
,![]() ;
;![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高一学生的视力健康状况,在高一年级体检活动中采用统一的标准对数视力表,按照《中国学生体质健康监测工作手册》的方法对1039名学生进行了视力检测,判断标准为:双眼裸眼视力![]() 为视力正常,
为视力正常, ![]() 为视力低下,其中
为视力低下,其中![]() 为轻度,
为轻度, ![]() 为中度,
为中度, ![]() 为重度.统计检测结果后得到如图所示的柱状图.
为重度.统计检测结果后得到如图所示的柱状图.
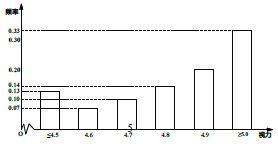
(1)求该校高一年级轻度近视患病率;
(2)根据保护视力的需要,需通知检查结果为“重度近视”学生的家长带孩子去医院眼科进一步检查和确诊,并开展相应的矫治,则该校高一年级需通知的家长人数约为多少人?
(3)若某班级6名学生中有2人为视力正常,则从这6名学生中任选2人,恰有1人视力正常的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校微信公众号收到非常多的精彩留言,学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(1)求这100位留言者年龄的平均数和中位数;
(2)学校从参加调查的年龄在![]() 和
和![]() 的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在
的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在![]() 的留言者每人一部价值1000元的手机,年龄在
的留言者每人一部价值1000元的手机,年龄在![]() 的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.
的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com