
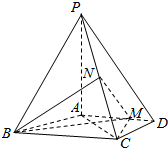
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.分析 (1)法一、取PB中点G,连接AG,NG,由三角形的中位线定理可得NG∥BC,且NG=$\frac{1}{2}BC$,再由已知得AM∥BC,且AM=$\frac{1}{2}$BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;
法二、证明MN∥平面PAB,转化为证明平面NEM∥平面PAB,在△PAC中,过N作NE⊥AC,垂足为E,连接ME,由已知PA⊥底面ABCD,可得PA∥NE,通过求解直角三角形得到ME∥AB,由面面平行的判定可得平面NEM∥平面PAB,则结论得证;
(2)连接CM,证得CM⊥AD,进一步得到平面PNM⊥平面PAD,在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.然后求解直角三角形可得直线AN与平面PMN所成角的正弦值.
解答 (1)证明:法一、如图,取PB中点G,连接AG,NG,
∵N为PC的中点,
∴NG∥BC,且NG=$\frac{1}{2}BC$,
又AM=$\frac{2}{3}AD=2$,BC=4,且AD∥BC,
∴AM∥BC,且AM=$\frac{1}{2}$BC,
则NG∥AM,且NG=AM,
∴四边形AMNG为平行四边形,则NM∥AG,
∵AG?平面PAB,NM?平面PAB,
∴MN∥平面PAB;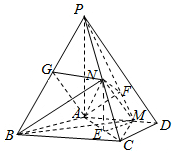
法二、
在△PAC中,过N作NE⊥AC,垂足为E,连接ME,
在△ABC中,由已知AB=AC=3,BC=4,得cos∠ACB=$\frac{{4}^{2}+{3}^{2}-{3}^{2}}{2×4×3}=\frac{2}{3}$,
∵AD∥BC,
∴cos$∠EAM=\frac{2}{3}$,则sin∠EAM=$\frac{\sqrt{5}}{3}$,
在△EAM中,
∵AM=$\frac{2}{3}AD=2$,AE=$\frac{1}{2}AC=\frac{3}{2}$,
由余弦定理得:EM=$\sqrt{A{E}^{2}+A{M}^{2}-2AE•AM•cos∠EAM}$=$\sqrt{\frac{9}{4}+4-2×\frac{3}{2}×2×\frac{2}{3}}=\frac{3}{2}$,
∴cos∠AEM=$\frac{(\frac{3}{2})^{2}+(\frac{3}{2})^{2}-4}{2×\frac{3}{2}×\frac{3}{2}}=\frac{1}{9}$,
而在△ABC中,cos∠BAC=$\frac{{3}^{2}+{3}^{2}-{4}^{2}}{2×3×3}=\frac{1}{9}$,
∴cos∠AEM=cos∠BAC,即∠AEM=∠BAC,
∴AB∥EM,则EM∥平面PAB.
由PA⊥底面ABCD,得PA⊥AC,又NE⊥AC,
∴NE∥PA,则NE∥平面PAB.
∵NE∩EM=E,
∴平面NEM∥平面PAB,则MN∥平面PAB;
(2)解:在△AMC中,由AM=2,AC=3,cos∠MAC=$\frac{2}{3}$,得CM2=AC2+AM2-2AC•AM•cos∠MAC=$9+4-2×3×2×\frac{2}{3}=5$.
∴AM2+MC2=AC2,则AM⊥MC,
∵PA⊥底面ABCD,PA?平面PAD,
∴平面ABCD⊥平面PAD,且平面ABCD∩平面PAD=AD,
∴CM⊥平面PAD,则平面PNM⊥平面PAD.
在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.
在Rt△PAC中,由N是PC的中点,得AN=$\frac{1}{2}PC$=$\frac{1}{2}\sqrt{P{A}^{2}+P{C}^{2}}=\frac{5}{2}$,
在Rt△PAM中,由PA•AM=PM•AF,得AF=$\frac{PA•AM}{PM}=\frac{4×2}{\sqrt{{4}^{2}+{2}^{2}}}=\frac{4\sqrt{5}}{5}$,
∴sin$∠ANF=\frac{AF}{AN}=\frac{\frac{4\sqrt{5}}{5}}{\frac{5}{2}}=\frac{8\sqrt{5}}{25}$.
∴直线AN与平面PMN所成角的正弦值为$\frac{8\sqrt{5}}{25}$.
点评 本题考查直线与平面平行的判定,考查直线与平面所成角的求法,考查数学转化思想方法,考查了空间想象能力和计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{2}$个单位长度 | B. | -π个单位长度 | C. | π个单位长度 | D. | $\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )
某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )| A. | 各月的平均最低气温都在0℃以上 | |
| B. | 七月的平均温差比一月的平均温差大 | |
| C. | 三月和十一月的平均最高气温基本相同 | |
| D. | 平均最高气温高于20℃的月份有5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1>0,0.6<q<0.7 | B. | a1<0,-0.7<q<-0.6 | ||
| C. | a1>0,0.7<q<0.8 | D. | a1<0,-0.8<q<-0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com