
分析 (Ⅰ)由条件利用等比数列的定义和性质,求得数列{an}为首项等于1、公比为q的等比数列,再根据2a2,a3,a2+2成等差数列求得公比q的值,可得{an}的通项公式.
(Ⅱ)利用双曲线的定义和简单性质求得en=$\sqrt{{1{+a}_{n}}^{2}}$,根据e2=$\frac{5}{3}$=$\sqrt{{1+q}^{2}}$,求得q的值,可得{an}的解析式,再利用放缩法可得∴en=$\sqrt{{1{+a}_{n}}^{2}}$>${(\frac{4}{3})}^{n-1}$,从而证得不等式成立.
解答 解:(Ⅰ)∵Sn+1=qSn+1 ①,∴当n≥2时,Sn=qSn-1+1 ②,两式相减可得an+1=q•an,
即从第二项开始,数列{an}为等比数列,公比为q.
当n=1时,∵数列{an}的首项为1,∴a1+a2=S2=q•a1+1,∴a2 =a1•q,
∴数列{an}为等比数列,公比为q.
∵2a2,a3,a2+2成等差数列,∴2a3 =2a2+a2+2,∴2q2=2q+q+2,求得q=2,或 q=-$\frac{1}{2}$.
根据q>0,故取q=2,∴an=2n-1,n∈N*.
(Ⅱ)证明:设双曲线x2-$\frac{{y}^{2}}{{a}_{n}^{2}}$=1的离心率为en,
∴en=$\frac{\sqrt{1{{+a}_{n}}^{2}}}{1}$=$\sqrt{{1{+a}_{n}}^{2}}$.
由于数列{an}为首项等于1、公比为q的等比数列,
∴e2=$\frac{5}{3}$=$\sqrt{{1{+a}_{2}}^{2}}$=$\sqrt{{1+q}^{2}}$,q=$\frac{4}{3}$,
∴an=${(\frac{4}{3})}^{n-1}$,∴en=$\sqrt{{1{+a}_{n}}^{2}}$=$\sqrt{1{+(\frac{4}{3})}^{2n-2}}$>$\sqrt{{(\frac{4}{3})}^{2n-2}}$=${(\frac{4}{3})}^{n-1}$.
∴e1+e2+???+en>1+$\frac{4}{3}$+${(\frac{4}{3})}^{2}$+…+${(\frac{4}{3})}^{n-1}$=$\frac{1{-(\frac{4}{3})}^{n}}{1-\frac{4}{3}}$=$\frac{{4}^{n}-{3}^{n}}{{3}^{n-1}}$,原不等式得证.
点评 本题主要考查等差数列、等比数列的定义和性质,用放缩法进行数列求和,双曲线的简单性质,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
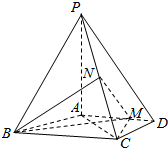 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com