
分析 (1)求出f(x)的导数,求得切线的斜率和切点,进而得到所求切线的方程;
(2)由f(x)=0,可得-c=x3+4x2+4x,由g(x)=x3+4x2+4x,求得导数,单调区间和极值,由-c介于极值之间,解不等式即可得到所求范围;
(3)先证若f(x)有三个不同零点,令f(x)=0,可得单调区间有3个,求出导数,由导数的图象与x轴有两个不同的交点,运用判别式大于0,可得a2-3b>0;再由a=b=4,c=0,可得若a2-3b>0,不能推出f(x)有3个零点.
解答 解:(1)函数f(x)=x3+ax2+bx+c的导数为f′(x)=3x2+2ax+b,
可得y=f(x)在点(0,f(0))处的切线斜率为k=f′(0)=b,
切点为(0,c),可得切线的方程为y=bx+c;
(2)设a=b=4,即有f(x)=x3+4x2+4x+c,
由f(x)=0,可得-c=x3+4x2+4x,
由g(x)=x3+4x2+4x的导数g′(x)=3x2+8x+4=(x+2)(3x+2),
当x>-$\frac{2}{3}$或x<-2时,g′(x)>0,g(x)递增;
当-2<x<-$\frac{2}{3}$时,g′(x)<0,g(x)递减.
即有g(x)在x=-2处取得极大值,且为0;
g(x)在x=-$\frac{2}{3}$处取得极小值,且为-$\frac{32}{27}$.
由函数f(x)有三个不同零点,可得-$\frac{32}{27}$<-c<0,
解得0<c<$\frac{32}{27}$,
则c的取值范围是(0,$\frac{32}{27}$);
(3)证明:若f(x)有三个不同零点,令f(x)=0,
可得f(x)的图象与x轴有三个不同的交点.
即有f(x)有3个单调区间,
即为导数f′(x)=3x2+2ax+b的图象与x轴有两个交点,
可得△>0,即4a2-12b>0,即为a2-3b>0;
若a2-3b>0,即有导数f′(x)=3x2+2ax+b的图象与x轴有两个交点,
当c=0,a=b=4时,满足a2-3b>0,
即有f(x)=x(x+2)2,图象与x轴交于(0,0),(-2,0),则f(x)的零点为2个.
故a2-3b>0是f(x)有三个不同零点的必要而不充分条件.
点评 本题考查导数的运用:求切线的方程和单调区间、极值,考查函数的零点的判断,注意运用导数求得极值,考考查化简整理的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{2}$个单位长度 | B. | -π个单位长度 | C. | π个单位长度 | D. | $\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )
某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图,图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃,下面叙述不正确的是( )| A. | 各月的平均最低气温都在0℃以上 | |
| B. | 七月的平均温差比一月的平均温差大 | |
| C. | 三月和十一月的平均最高气温基本相同 | |
| D. | 平均最高气温高于20℃的月份有5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
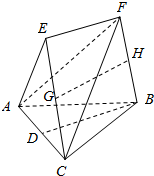 在如图所示的几何体中,D是AC的中点,EF∥DB.
在如图所示的几何体中,D是AC的中点,EF∥DB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com