
分析 (1)由f(x+2)=-f(x)可推知f(x+4)=f(x)得证.
(2)依题意求出f(x)在[-1,3)上的解析式,进而求出f(x)=-$\frac{1}{2}$时x的值.再根据函数的周期性求出在[0,2014]上的所有x的个数.
解答 解:(1)证明:∵f(x+2)=-f(x)
∴f(x+4)=f(x+2+2)=-f(x+2)=f(x)
∴f(x)是以4为周期的函数.
(2)当0≤x≤1时,f(x)=$\frac{1}{2}$x,
设-1≤x≤0,则0≤-x≤1,
∴f(-x)=(-x)=-x.
∵f(x)是奇函数,
∴f(-x)=-f(x),
∴-f(x)=-$\frac{1}{2}$x,即f(x)=$\frac{1}{2}$x.
故f(x)=$\frac{1}{2}$x(-1≤x≤1)
又设1<x<3,则-1<x-2<1,
∴f(x-2)=$\frac{1}{2}$(x-2),
又∵f(x-2)=-f(2-x)=-f[(-x)+2]=-[-f(-x)]=-f(x),
∴-f(x)=$\frac{1}{2}$(x-2),∴f(x)=-$\frac{1}{2}$(x-2)(1<x<3).
∴f(x)=$\left\{\begin{array}{l}{\frac{1}{2}x,-1≤x≤1}\\{-\frac{1}{2}(x-2),1<x<3}\end{array}\right.$,
由f(x)=-$\frac{1}{2}$,解得x=-1.
∵f(x)是以4为周期的周期函数.故f(x)=-$\frac{1}{2}$的所有x=4n-1(n∈Z).令0≤4n-1≤2014,则$\frac{1}{4}$≤n≤503,
又∵n∈Z,∴1≤n≤503(n∈Z),
∴在[0,2014]上共有503个x使f(x)=-$\frac{1}{2}$.
点评 本题主要考查了函数的周期性.在解题的时候,要注意函数在不同区间上不同的解析式,这是容易出错的地方.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | a为正相关,b为负相关,c为不相关 | B. | a为负相关,b为不相关,c为正相关 | ||
| C. | a为负相关,b为正相关,c为不相关 | D. | a为正相关,b为不相关,c为负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
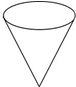
| A. | 主视图和左视图是三角形,俯视图是圆 | |
| B. | 主视图和左视图是三角形,俯视图是圆和圆心 | |
| C. | 主视图是圆和圆心,俯视图和左视图是三角形 | |
| D. | 主视图和俯视图是三角形,左视图是圆和圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com