
【题目】如图,已知边长为2的正三角形ABE所在的平面与菱形ABCD所在的平面垂直,且![]() ,点F是BC上一点,且
,点F是BC上一点,且![]() .
.
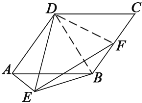
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)是否存在一个常数k,使得三棱锥![]() 的体积等于四棱锥
的体积等于四棱锥![]() 的体积的
的体积的![]() ,若存在,求出k的值;若不存在,说明理由.
,若存在,求出k的值;若不存在,说明理由.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】
已知函数![]()
![]() 有极值,且函数
有极值,且函数![]() 的极值点是
的极值点是![]() 的极值点,其中
的极值点,其中![]() 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若函数
时,若函数![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)![]() (c≠0),其图象的对称中心为(
(c≠0),其图象的对称中心为(![]() ,
,![]() ),现已知f(x)
),现已知f(x)![]() ,数列{an}的通项公式为an=f(
,数列{an}的通项公式为an=f(![]() )(n∈N+),则此数列前2020项的和为_____.
)(n∈N+),则此数列前2020项的和为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记![]() 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,![]() 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数![]() 在区间
在区间![]() 上存在零点;
上存在零点;
②要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象向左平移
的图象向左平移![]() 个单位;
个单位;
③若![]() ,则函数
,则函数![]() 的值城为
的值城为![]() ;
;
④“![]() ”是“函数
”是“函数![]() 在定义域上是奇函数”的充分不必要条件;
在定义域上是奇函数”的充分不必要条件;
⑤已知![]() 为等差数列,若
为等差数列,若![]() ,且它的前
,且它的前![]() 项和
项和![]() 有最大值,那么当
有最大值,那么当![]() 取得最小正值时,
取得最小正值时,![]() .
.
其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() .
.
(1)求直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 在圆
在圆![]() 上运动,
上运动,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求证:![]() 为定值及动点
为定值及动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)不在![]() 轴上的
轴上的![]() 点为
点为![]() 上任意一点,
上任意一点,![]() 与
与![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 交
交![]() 于另外一点
于另外一点![]() .求证:直线
.求证:直线![]() 与直线
与直线![]() 的斜率的乘积为定值,并求出该定值.
的斜率的乘积为定值,并求出该定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com